Este tópico visa conectar propriedades macroscópicas dos gases (como pressão e temperatura) com propriedades microscópicas, associadas aos seus constituintes, como átomos e moléculas, como, por exemplo, suas velocidades. Certamente não contabilizaremos as velocidades de cada partícula do sistema porque isso seria impossível, mas trataremos de médias, ou seja, existe uma proximidade desse assunto com a termodinâmica estatística.
Antes de começar, é importante especificar algumas características do modelo cinético dos gases:
- Um gás seria composto por partículas esféricas com mesma massa e com mesmo tamanho, sendo este último desprezível em comparação com o volume do recipiente.
- O movimento das partículas é totalmente aleatório, sem privilegiar nenhuma direção específica no espaço.
- As partículas não interagem umas com as outras, exceto nas colisões, que são elásticas, ou seja, conservam a energia cinética total das partículas interagentes.
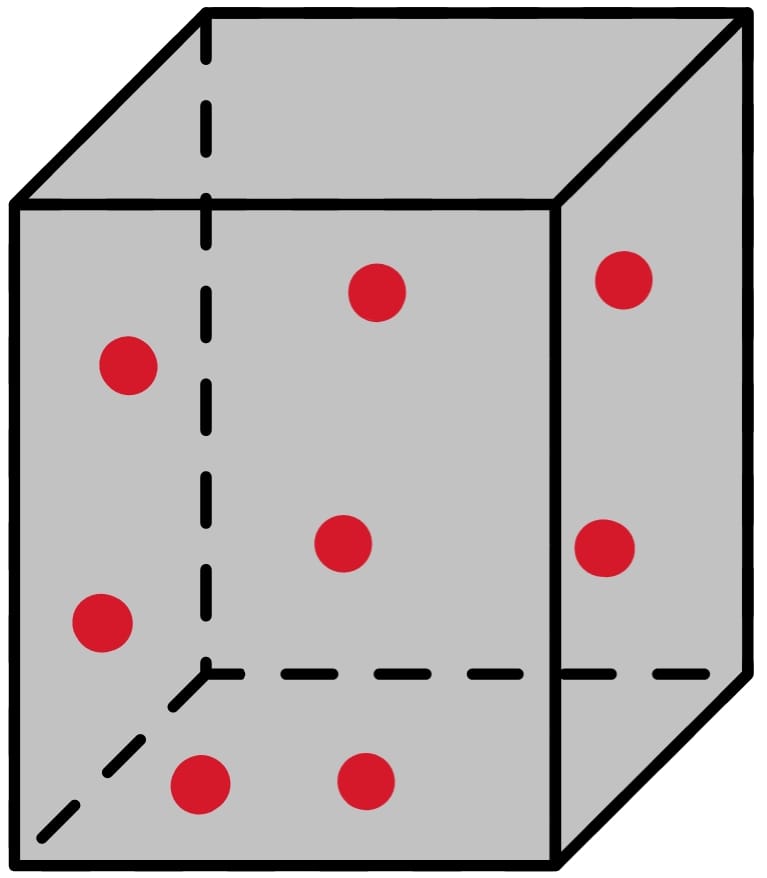
A primeira propriedade macroscópica a ser calculada é a pressão do gás. O caminho que seguiremos é escolher uma partícula do sistema e calcular a mudança de momento linear sofrida por essa partícula quando ela colide com a parede do recipiente. Depois, estabeleceremos um intervalo de tempo e calcularemos quantas vezes ela colide com essa parede por unidade de tempo. Multiplicaremos esse resultado pela mudança de momento de cada colisão, que é a força. Por último, dividiremos essa força pela área de colisão e teremos a pressão exercida pela partícula escolhida. Para calcular a pressão total, estenderemos o raciocínio para todas as partículas do sistema.
O vetor velocidade de uma partícula ![]() tem três componentes:
tem três componentes: ![]() ,
, ![]() e
e ![]() , de forma vale a soma vetorial:
, de forma vale a soma vetorial:
![]()
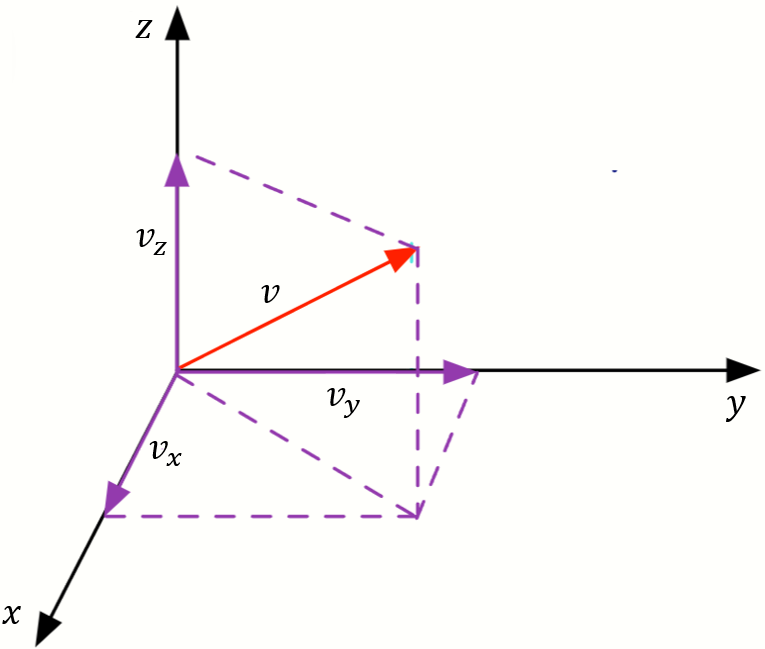
De modo que, por teorema de Pitágoras:
![]()
Vamos considerar que a partícula ![]() se movimente em direção à parede ABCD, paralela ao plano
se movimente em direção à parede ABCD, paralela ao plano ![]() , na imagem abaixo:
, na imagem abaixo:

Perceba que o choque muda a direção de ![]() (de
(de ![]() para
para ![]() ), mas não de
), mas não de ![]() e
e ![]() . Isso não afeta
. Isso não afeta ![]() , pois este vetor depende dos quadrados dos módulos dos componentes, de forma que:
, pois este vetor depende dos quadrados dos módulos dos componentes, de forma que:
![]()
O momento linear antes da colisão é:
![]()
Após a colisão:
![]()
Porém:
![]()
Porém:
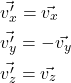
De modo que a variação de momento é:
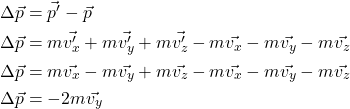
Em módulo:
![]()
Esta é a mudança de momento que a partícula ![]() sofre em cada colisão. Repare que não estamos falando de
sofre em cada colisão. Repare que não estamos falando de ![]() , mas de
, mas de ![]() . Não estranhe o fato de
. Não estranhe o fato de ![]() depender só de
depender só de ![]() , pois isso é consequência do fato de apenas a componente
, pois isso é consequência do fato de apenas a componente ![]() mudar na colisão.
mudar na colisão.
Calculamos a mudança de momento para uma única colisão, mas a partícula ![]() colide com esse recipiente várias vezes em um intervalo
colide com esse recipiente várias vezes em um intervalo ![]() . O número de colisões por unidade de tempo (chamado de frequência de colisões) que essa partícula faz com a parede ABCD depende de quantas vezes o dobro do segmento
. O número de colisões por unidade de tempo (chamado de frequência de colisões) que essa partícula faz com a parede ABCD depende de quantas vezes o dobro do segmento ![]() cabe dentro do valor da velocidade. Isso pode parecer abstrato, mas vamos trabalhar com números. Suponha que
cabe dentro do valor da velocidade. Isso pode parecer abstrato, mas vamos trabalhar com números. Suponha que ![]() e que a partícula tenha velocidade
e que a partícula tenha velocidade ![]() . Para ir até a parede oposta e voltar até ABCD para uma nova colisão, é necessário percorrer o dobro de
. Para ir até a parede oposta e voltar até ABCD para uma nova colisão, é necessário percorrer o dobro de ![]() :
: ![]() . Quantas vezes
. Quantas vezes ![]() cabe dentro de
cabe dentro de ![]() ? 10 vezes! Assim, a partícula consegue colidir, por segundo, dez vezes com a parede ABCD. Generalizando (saindo do exemplo numérico), o número de colisões, por unidade de tempo, que a partícula realiza na parede ABCD é:
? 10 vezes! Assim, a partícula consegue colidir, por segundo, dez vezes com a parede ABCD. Generalizando (saindo do exemplo numérico), o número de colisões, por unidade de tempo, que a partícula realiza na parede ABCD é:
![]()
Em cada uma dessas colisões a mudança de momento é ![]() , então, a mudança total de momento sofrida pela partícula
, então, a mudança total de momento sofrida pela partícula ![]() por unidade de tempo é:
por unidade de tempo é:
![]()
Essa grandeza tem unidade no SI:
![]()
Essa grandeza é a taxa de variação temporal do momento. Pela segunda lei de Newton essa taxa é a força:
![]()
Então a força que age entre a partícula e a parede tem módulo:
![]()
Sabemos que a pressão é essa força por unidade de área:
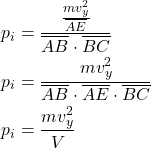
Estendendo esse resultado para todas as partículas do recipiente, temos que a pressão total é:
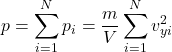
Vamos definir agora a primeira grandeza estatística do assunto: ![]() , que é a média dos valores de
, que é a média dos valores de ![]() de todas as partículas do recipiente:
de todas as partículas do recipiente:
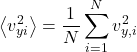
E podemos isolar a somatória:
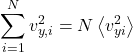
De modo que a pressão total é:
![]()
Podemos escrever esse resultado em função de ![]() , se considerarmos a condição isotrópica do sistema. Ela faz referência a uma das características citadas no início deste tópico, mais especificamente o fato de não existir uma direção preferencial:
, se considerarmos a condição isotrópica do sistema. Ela faz referência a uma das características citadas no início deste tópico, mais especificamente o fato de não existir uma direção preferencial: ![]() ,
, ![]() ou
ou ![]() . Quantitativamente, essa propriedade é descrita por:
. Quantitativamente, essa propriedade é descrita por:
![]()
Como definimos no início:
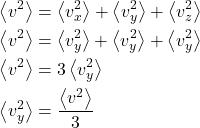
E a pressão total se torna:
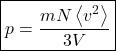
Este é o primeiro resultado importante da teoria cinética: o valor da pressão em função da média de ![]() das partículas. Repare que quanto maior essa média, maior é a pressão, o que é coerente com nossa intuição, uma vez que a violência das colisões cresce com essa média. A dependência com
das partículas. Repare que quanto maior essa média, maior é a pressão, o que é coerente com nossa intuição, uma vez que a violência das colisões cresce com essa média. A dependência com ![]() também é coerente: uma redução de volume produzirá um aumento de pressão. O aumento de
também é coerente: uma redução de volume produzirá um aumento de pressão. O aumento de ![]() também provoca um aumento de pressão, pelo aumento do número de colisões com as paredes do recipiente. A dependência com a massa também é óbvia, pois partículas mais pesadas exercem mais força nas paredes. Podemos reescrever essa expressão de maneira conveniente:
também provoca um aumento de pressão, pelo aumento do número de colisões com as paredes do recipiente. A dependência com a massa também é óbvia, pois partículas mais pesadas exercem mais força nas paredes. Podemos reescrever essa expressão de maneira conveniente:
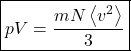
Teorema da Equipartição da Energia
Para um sistema em equilíbrio a uma temperatura ![]() , a energia está igualmente distribuída em seus graus de liberdade em parcelas iguais à
, a energia está igualmente distribuída em seus graus de liberdade em parcelas iguais à ![]() , onde
, onde ![]() é a constante de Boltzmann:
é a constante de Boltzmann: ![]() .
.
Você deve estar se perguntando o que é um grau de liberdade. Existem muitas formas das partículas de um sistema apresentarem energia. Uma delas é a energia cinética (que depende de ![]() ). Outra é a energia rotacional (que depende de
). Outra é a energia rotacional (que depende de ![]() , onde
, onde ![]() é a velocidade angular da molécula). Outra é a energia vibracional (boa parte dela proporcional à
é a velocidade angular da molécula). Outra é a energia vibracional (boa parte dela proporcional à ![]() , onde
, onde ![]() é o comprimento da ligação). A energia luminosa, por exemplo, está associada aos quadrados dos campos elétrico (
é o comprimento da ligação). A energia luminosa, por exemplo, está associada aos quadrados dos campos elétrico (![]() ) e magnético (
) e magnético (![]() ), de acordo com a teoria clássica. Cada um desses termos quadráticos é um grau de liberdade e concentra
), de acordo com a teoria clássica. Cada um desses termos quadráticos é um grau de liberdade e concentra ![]() por molécula.
por molécula.
Como um gás ideal monoatômico só contém a contribuição translacional ![]() (desprezando a energia eletrônica), podemos dizer que cada componente da energia cinética (dependente de
(desprezando a energia eletrônica), podemos dizer que cada componente da energia cinética (dependente de ![]() ,
, ![]() e
e ![]() ) contribui com
) contribui com ![]() . A energia translacional de uma partícula em um gás perfeito é, então:
. A energia translacional de uma partícula em um gás perfeito é, então:
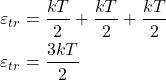
Para ![]() moléculas:
moléculas:
![]()
A constante de Boltzmann, quando multiplicada pela constante de Avogadro, fornece sua versão molar, bem conhecida desde os primeiros tópicos de Química: a constante universal dos gases. Assim:
![]()
Se multiplicarmos e dividirmos a expressão que tínhamos obtido pelo número de Avogadro, surge a constante dos gases e o número de mols de gás:
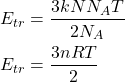
Como a energia interna de um gás perfeito monoatômico se deve apenas à contribuição cinética:
![]()
E a capacidade calorífica a volume constante (![]() ) de um gás perfeito monoatômico é:
) de um gás perfeito monoatômico é:
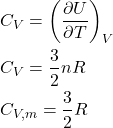
Como ![]() :
:
![]()
Que são resultados bem conhecidos da termodinâmica clássica.
A energia translacional média é dada por:
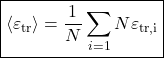
De modo que:
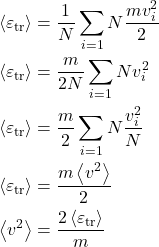
E o produto ![]() se torna:
se torna:
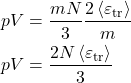
Do teorema da equipartição:
![]()
E temos:
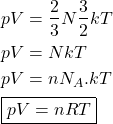
Que é outro importante resultado. A lei do gás ideal é conhecida por ter sido alcançada empiricamente, ou seja, por meio de observações experimentais. Veja que argumentos estatísticos e microscópicos nos levaram à mesma equação.
A velocidade quadrática média ![]() é definida como:
é definida como:
![]()
A partir da energia translacional média:
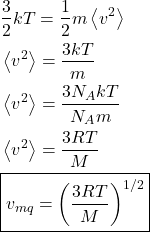
A Distribuição de Velocidades
Seria esperar muito que as partículas de um gás tenham a mesma velocidade. Certamente muitas moléculas têm velocidades acima da média e outras muitas moléculas possuem velocidades abaixo da média. Poderíamos abordar o problema contando o número de moléculas que possuem, por exemplo, velocidade igual a ![]() . No entanto, como a velocidade é contínua, esse número é aproximadamente zero. É mais fácil contabilizar o número de moléculas com velocidade entre
. No entanto, como a velocidade é contínua, esse número é aproximadamente zero. É mais fácil contabilizar o número de moléculas com velocidade entre ![]() e
e ![]() , ou seja, em uma faixa de largura
, ou seja, em uma faixa de largura ![]() . Por, exemplo, poderíamos contar o número de moléculas do gás que possuem velocidades entre
. Por, exemplo, poderíamos contar o número de moléculas do gás que possuem velocidades entre ![]() e
e ![]() .
.
Se o número de moléculas com velocidades dentreo de um intervalo de velocidades de largura ![]() for
for ![]() , a probabilidade de escolhermos uma molécula com velocidade neste intervalo é de
, a probabilidade de escolhermos uma molécula com velocidade neste intervalo é de ![]() . Como essa probabilidade aumenta com a largura
. Como essa probabilidade aumenta com a largura ![]() do intervalo, temos que:
do intervalo, temos que:
![]()
A relação completa é escrita adicionando uma função chamada função de distribuição de velocidades ![]() :
:
![]()
Perceba que ![]() é uma densidade de probabilidade, no sentido que ela é a probabilidade por unidade de intervalo de
é uma densidade de probabilidade, no sentido que ela é a probabilidade por unidade de intervalo de ![]() .
. ![]() nos fornece a probabilidade de escolhermos uma molécula do sistema com velocidade no intervalo entre
nos fornece a probabilidade de escolhermos uma molécula do sistema com velocidade no intervalo entre ![]() e
e ![]() . Essa probabilidade é infinitesimal porque a largura do intervalo também o é. Para um intervalo finito de velocidades, a probabilidade é:
. Essa probabilidade é infinitesimal porque a largura do intervalo também o é. Para um intervalo finito de velocidades, a probabilidade é:
![]()
Se tomarmos esse intervalo de velocidade como ![]() , temos
, temos ![]() de probabilidade, pois todas as moléculas possuem velocidade nesse intervalo. Esta é a origem da condição de normalização:
de probabilidade, pois todas as moléculas possuem velocidade nesse intervalo. Esta é a origem da condição de normalização:
![]()
A forma matemática de ![]() foi deduzida pela primeira vez por James Maxwell, em 1860 e, usando argumentos diferentes, pelo mesmo Maxwell e por Boltzmann, alguns anos depois. A dedução é um pouco tediosa e não será posta aqui. A essência é considerar que
foi deduzida pela primeira vez por James Maxwell, em 1860 e, usando argumentos diferentes, pelo mesmo Maxwell e por Boltzmann, alguns anos depois. A dedução é um pouco tediosa e não será posta aqui. A essência é considerar que ![]() ,
, ![]() e
e ![]() são independentes, a distribuição é isotrópica, depende apenas do módulo da velocidade e definir um espaço de velocidades, um espaço abstrato cujas coordenadas espaciais
são independentes, a distribuição é isotrópica, depende apenas do módulo da velocidade e definir um espaço de velocidades, um espaço abstrato cujas coordenadas espaciais ![]() são lugar à duas primeiras derivadas temporais, ou seja,
são lugar à duas primeiras derivadas temporais, ou seja, ![]() . A função
. A função ![]() é mostrada abaixo (na forma molar e na forma molecular):
é mostrada abaixo (na forma molar e na forma molecular):
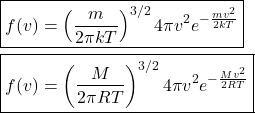
O gráfico de ![]() (mostrada abaixo) apresentra propriedades interessantes.
(mostrada abaixo) apresentra propriedades interessantes.
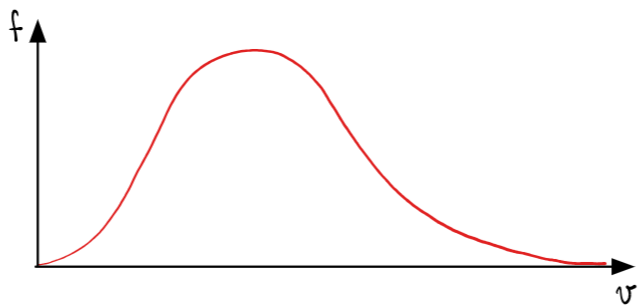
- A probabilidade de escolhermos uma partícula com velocidade extremamente grande é próxima de zero. Matematicamente isso ocorre devido ao termo exponencial, que apresenta
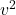 no expoente negativo, fazendo
no expoente negativo, fazendo 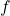 cair muito rápido.
cair muito rápido. - A probabilidade de escolhermos uma partícula com velocidade muito pequena também é pequena. A razão matemática é que a exponencial tende à
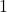 quando
quando  diminui muito, enquanto
diminui muito, enquanto 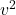 tende à zero, fazendo
tende à zero, fazendo 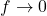 .
. - É muito pouco provável que moléculas pesadas tenham altíssimas velocidades, porque o expoente da exponencial seria muito negativo, diminuindo
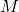 .
. - O aquecimento faz o expoente da exponencial ser menos negativo e suaviza a queda de
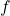 .
.
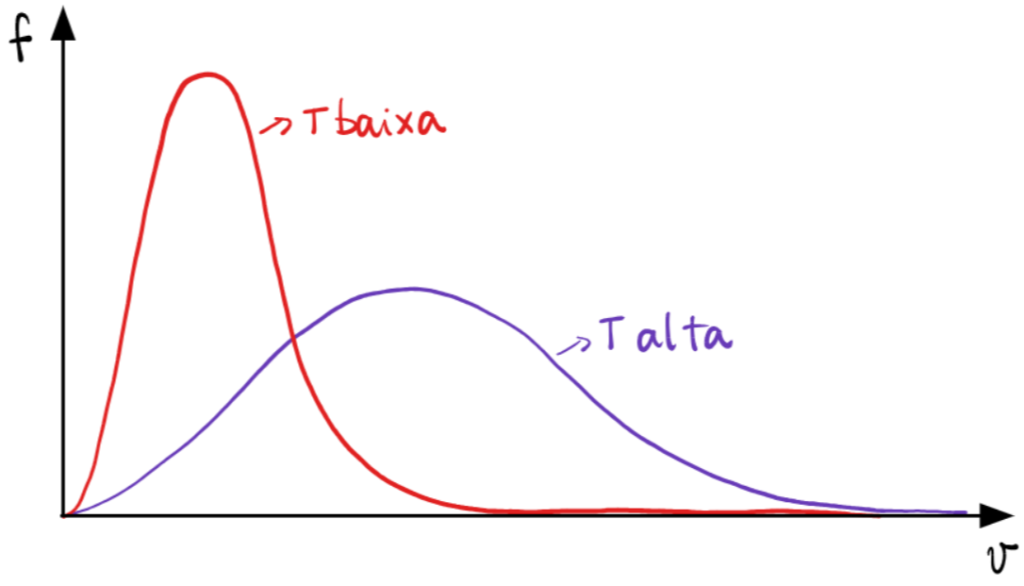
Perceba que, olhando para as duas curvas acima, há uma maior probabilidade de encontrarmos moléculas a partir de um certo valor de velocidade.
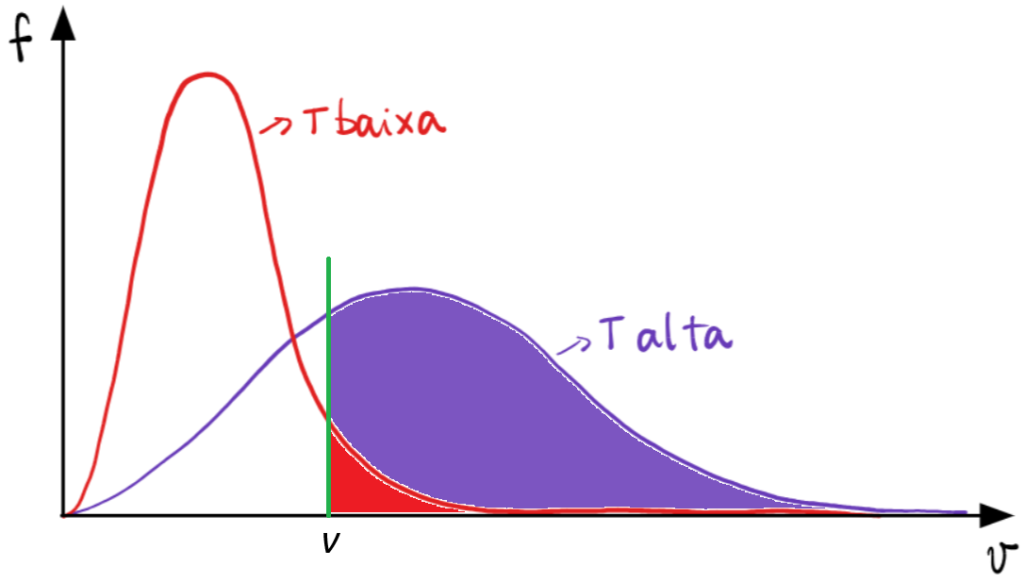
Essas observações foram comprovadas experimentalmente, fazendo as moléculas de gases que saíram de um forno serem “filtradas” por suas velocidades. Simplificadamente, essa separação é feita por um seletor em movimento circular com velocidade angular controlada. Para uma dada velocidade angular, um certo número de marcações surge no detector, indicando o número de partículas com velocidade compatível com aquela rotação específica do seletor.
Aplicações
Suponha uma sala de aula com ![]() alunos com idades
alunos com idades ![]() :
: ![]() ,
, ![]() , … A idade média da turma é a soma das idades divida pelo número de alunos. Muito provavelmente algumas idades se repetirão e a média será ponderada pelo número de repetições de cada idade.
, … A idade média da turma é a soma das idades divida pelo número de alunos. Muito provavelmente algumas idades se repetirão e a média será ponderada pelo número de repetições de cada idade.
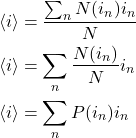
Onde ![]() é a probabilidade de escolhermos um aluno com idade
é a probabilidade de escolhermos um aluno com idade ![]() e vemos que a média das idades pode ser calculada pela soma de termos com o formato: probabilidade x idade.
e vemos que a média das idades pode ser calculada pela soma de termos com o formato: probabilidade x idade.
Poderíamos ter interesse na média dos quadrados das idades. O procedimento seria o mesmo:
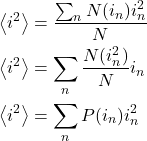
Fica claro que, se quisermos a média de qualquer potência da idade (![]() ), podemos tomar uma soma com parcelas de formato “probabilidade x potência da idade”.
), podemos tomar uma soma com parcelas de formato “probabilidade x potência da idade”.
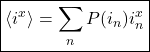
No contexto dos gases, podemos calcular a média de ![]() usando a mesma argumentação. Como as velocidades variam continuamente, a soma dá lugar a uma integral, de forma que:
usando a mesma argumentação. Como as velocidades variam continuamente, a soma dá lugar a uma integral, de forma que:
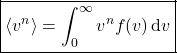
Ou seja, pelo fato de ![]() representar uma probabilidade, podemos usá-la para calcular o valor médio de qualquer potência de
representar uma probabilidade, podemos usá-la para calcular o valor médio de qualquer potência de ![]() , de modo que
, de modo que ![]() tem um papel preditivo para
tem um papel preditivo para ![]() .
.
A velocidade média, por exemplo, é:
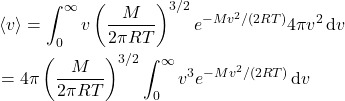
Essa integral é conhecida e pode ser encontrada em qualquer tabela de integrais:
![]()
Ao usar ![]() e
e ![]() (pratique), encontramos que:
(pratique), encontramos que:
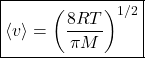
Para ![]() :
:
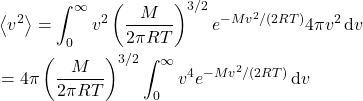
Ao usar a integral abaixo:
![]()
Chegamos em:
![]()
Que é exatamente o que já havíamos obtido no início do tópico. A velocidade quadrática média é, lembrando, a raiz quadrada deste valor:
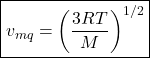
O máximo de ![]() nos dá a velocidade mais provável (
nos dá a velocidade mais provável (![]() ), facilmente encontrada pela primeira derivada de
), facilmente encontrada pela primeira derivada de ![]() em relação a
em relação a ![]() :
:

Não será demonstrado aqui (porque foge ao objetivo deste tópico), mas a velocidade relativa (![]() ) pode ser calculada por:
) pode ser calculada por:
![]()
Colisões
A teoria cinética também nos permite calcular a frequência de colisões, ou seja, o número de colisões que uma partícula sofre por unidade de tempo. Para tal, imaginemos que cada partícula, ao movimentar-se, carrega, ao redor de si, uma seção de choque ![]() , ou seja, um círculo de raio
, ou seja, um círculo de raio ![]() (o diâmetro da partícula), onde
(o diâmetro da partícula), onde ![]() . Quando essa partícula se movimenta, a seção de choque varre uma distância, gerando um cilindro de área da base
. Quando essa partícula se movimenta, a seção de choque varre uma distância, gerando um cilindro de área da base ![]() e altura igual à distância percorrida pela partícula. Essa distância pode ser calculada, considerando que a partícula se movimenta em relação à outra com velocidade
e altura igual à distância percorrida pela partícula. Essa distância pode ser calculada, considerando que a partícula se movimenta em relação à outra com velocidade ![]() e a outra está parada. Como “distânica = velocidade x tempo”, a distância percorrida pela partícula é
e a outra está parada. Como “distânica = velocidade x tempo”, a distância percorrida pela partícula é ![]() .
.
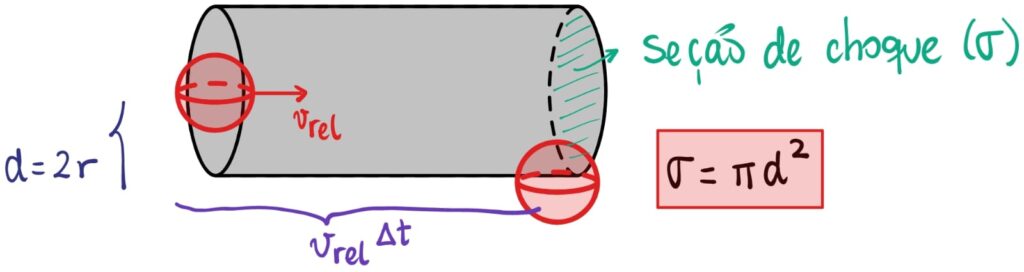
A partícula parada será colidida pela partícula em movimento se o seu centro entrar nesse cilindro, ou seja, se o centro da partícula estiver a uma distância igual ou menor que ![]() do centro da partícula em movimento. Leia este parágrafo olhando o desenho acima e tente entender, pois é um ponto importante.
do centro da partícula em movimento. Leia este parágrafo olhando o desenho acima e tente entender, pois é um ponto importante.
O volume do cilindro é ![]() . Considerando que a densidade de partículas seja representada por
. Considerando que a densidade de partículas seja representada por ![]() , o número de partículas nesse cilindro é a densidade de partículas multiplicada pelo volume do cilindro (
, o número de partículas nesse cilindro é a densidade de partículas multiplicada pelo volume do cilindro (![]() ). Como a frequência de colisões
). Como a frequência de colisões ![]() é o número de partículas que entram nesse cilindro por unidade de tempo:
é o número de partículas que entram nesse cilindro por unidade de tempo:
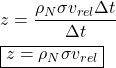
Perceba que ![]() tem unidades de
tem unidades de ![]() ou
ou ![]() , como deve ser (ao conferir, não se esqueça que
, como deve ser (ao conferir, não se esqueça que ![]() tem unidades de
tem unidades de ![]() ). Pode-se observar, ainda, que
). Pode-se observar, ainda, que ![]() aumenta com a densidade de partículas e com a velocidade média, como deve ser. Para gases ideais, sabemos calcular
aumenta com a densidade de partículas e com a velocidade média, como deve ser. Para gases ideais, sabemos calcular ![]() :
:
![]()
E a frequência das colisões se torna:
![]()
Outra importante propriedade que pode ser derivada da teoria cinética dos gases é o livre caminho médio (![]() ). Ele é definido como a distância média percorrida pelas partículas de um gás sem sofrer nenhuma colisão.
). Ele é definido como a distância média percorrida pelas partículas de um gás sem sofrer nenhuma colisão.
O tempo que a partícula passa sem colidir com nenhuma outra é inversamente proporcional à ![]() , ou seja, quanto maior o valor de
, ou seja, quanto maior o valor de ![]() , menos tempo a partícula pode mover-se sem interrupções. Se
, menos tempo a partícula pode mover-se sem interrupções. Se ![]() , por exemplo, isso significa que ocorrem 20 colisões por segundo para a partícula. O inverso desse número é
, por exemplo, isso significa que ocorrem 20 colisões por segundo para a partícula. O inverso desse número é ![]() é
é ![]() , que significa que a cada
, que significa que a cada ![]() uma colisão ocorre. Ou seja, o tempo que a partícula passa sem colidir com nenhuma outra é simplesmente o inverso da frequência de colisões:
uma colisão ocorre. Ou seja, o tempo que a partícula passa sem colidir com nenhuma outra é simplesmente o inverso da frequência de colisões:
![]()
Como a distância que a partícula percorre nesse tempo é justamente o livre caminho médio ![]() , podemos usar cinemática básica para calcular
, podemos usar cinemática básica para calcular ![]() :
:
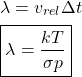
Observe que partículas com grandes seções de choque apresentam menores valores de ![]() , o que é totalmente coerente. É importante dizer que
, o que é totalmente coerente. É importante dizer que ![]() não depende da temperatura, diferente do que a expressão sugere. O que ocorre é que
não depende da temperatura, diferente do que a expressão sugere. O que ocorre é que ![]() também cresce com a temperatura, de modo que aquecer aumenta
também cresce com a temperatura, de modo que aquecer aumenta ![]() e aumenta proporcionalmente
e aumenta proporcionalmente ![]() . Como essas quantidades são divididas uma pela outra, a razão é sempre constante.
. Como essas quantidades são divididas uma pela outra, a razão é sempre constante.
Exercícios
1) Calcule a pressão exercida por ![]() partículas de gás, cada uma com massa de
partículas de gás, cada uma com massa de ![]() , em um recipiente de volume
, em um recipiente de volume ![]() . A velocidade quadrática média é
. A velocidade quadrática média é ![]() .
.
Gabarito
![]()
Resolução
2) Um bulbo com capacidade de ![]() contém
contém ![]() moléculas gasosas de hidrogênio e a pressão exercida por estas moléculas é
moléculas gasosas de hidrogênio e a pressão exercida por estas moléculas é ![]() . Calcule a média de
. Calcule a média de ![]() e a temperatura.
e a temperatura.
Gabarito
![]() e
e ![]() .
.
Resolução
3) Para um gás contendo ![]() moléculas (cada uma com massa de
moléculas (cada uma com massa de ![]() ) em um volume de
) em um volume de ![]() , calcule:
, calcule:
a) A energia cinética total das moléculas se sua velocidade quadrática média é ![]() .
.
b) Qual será sua temperatura?
Gabarito
a) ![]()
b) ![]()
Resolução
4) Calcule a energia cinética total de ![]() de um gás ideal no ponto de fusão normal da água.
de um gás ideal no ponto de fusão normal da água.
Gabarito
![]()
Resolução
5) Calcule a fração de moléculas de ![]() a
a ![]() e
e ![]() cujas velocidades estão no intervalo de
cujas velocidades estão no intervalo de ![]() a
a ![]() , onde
, onde ![]() é a velocidade mais provável.
é a velocidade mais provável.
Gabarito
![]()
Resolução
6) Organize as velocidades quadrática média, mais provável e média em ordem decrescente de valor.
Gabarito
![]()
Resolução
7) Calcule as velocidades quadrática média, média e mais provável das moléculas de ![]() . A densidade do gás a
. A densidade do gás a ![]() é
é ![]() (=
(= ![]() ). Considere comportamento ideal.
). Considere comportamento ideal.
Gabarito
![]()
![]()
![]()
Resolução
8) A molécula de oxigênio possui raio igual a ![]() . Calcule a seção de choque dessa molécula e o livre caminho médio, nas condições de
. Calcule a seção de choque dessa molécula e o livre caminho médio, nas condições de ![]() e
e ![]() .
.
Gabarito
![]()
![]()
Resolução
9) O livre caminho médio da molécula de um certo gás a ![]() é
é ![]() . O diâmetro de colisão da molécula é
. O diâmetro de colisão da molécula é ![]() . Calcule:
. Calcule:
a) A pressão do gás.
b) O número de moléculas por unidade de volume do gás.
Gabarito
![]() e
e ![]()
