Equações de Gibbs
As funções de estado que vimos até agora são: ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() . Podemos escrever:
. Podemos escrever:
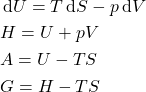
A variação de ![]() é:
é:
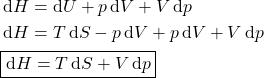
A variação de ![]() é:
é:
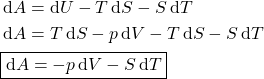
A variação de ![]() é:
é:
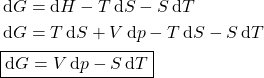
Em resumo, as relações de Gibbs são dadas pelas equações 1.
(1) 
Cada uma dessas relações mostra que ![]() ,
, ![]() ,
, ![]() e
e ![]() pode ser escrita como função de duas variáveis cada. Do cálculo, a variação de uma função
pode ser escrita como função de duas variáveis cada. Do cálculo, a variação de uma função ![]() é dada pela equação 2.
é dada pela equação 2.
(2) 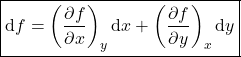
Observando as relações de Gibbs:
(3) ![]()
(4) ![]()
(5) ![]()
(6) ![]()
Da equação de Gibbs para ![]() , obtemos as equações 7. Repare que uma delas é a definição termodinâmica de temperatura, mas não será abordado em detalhes aqui porque envolve argumentos estatísticos.
, obtemos as equações 7. Repare que uma delas é a definição termodinâmica de temperatura, mas não será abordado em detalhes aqui porque envolve argumentos estatísticos.
(7) 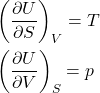
Da equação de Gibbs para ![]() , obtemos as equações 8.
, obtemos as equações 8.
(8) 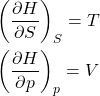
Da equação de Gibbs para ![]() , obtemos as equações 9.
, obtemos as equações 9.
(9) 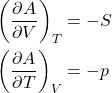
Da equação de Gibbs para ![]() , obtemos as equações 10.
, obtemos as equações 10.
(10) 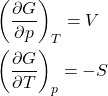
As Relações de Maxwell
Para uma função de duas variáveis:
![Rendered by QuickLaTeX.com \begin{align*}\left[\pdv{x}\left(\pdv{f}{y}\right)_x\right]_y = \left[\pdv{y}\left(\pdv{f}{x}\right)_y\right]_x\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-9fd078a76228ae8636fdf41f83bcb91e_l3.png)
Da equação de Gibbs para ![]() :
:
![]()
Usando as equações 7:
![]()
Da equação de Gibbs para ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}\left[\pdv{p}\left(\pdv{H}{S}\right)_p\right]_S = \left[\pdv{S}\left(\pdv{H}{p}\right)_S\right]_p\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-8900fd7bec22377266220823d58d9230_l3.png)
Usando as equações 8:
![]()
Da equação de Gibbs para ![]() :
:
![]()
Usando as equações 9:
![]()
Da equação de Gibbs para ![]() :
:
![Rendered by QuickLaTeX.com \begin{align*}\left[\pdv{p}\left(\pdv{G}{T}\right)_p\right]_T = \left[\pdv{T}\left(\pdv{G}{p}\right)_T\right]_p\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-0d27f1f7fd6df94fa90e2639046a3252_l3.png)
Usando as equações 10:
![]()
As quatro equações obtidas são chamadas relações de Maxwell:
(11) 
Variações Isotérmicas de Entropia
As duas primeiras relações de Maxwell são menos usadas em Química, mas as duas últimas fornece variações isotérmicas de entropia com ![]() e
e ![]() . Do primeiro tópico deste curso:
. Do primeiro tópico deste curso:
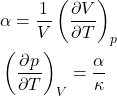
E escrevemos essas variações isotérmicas de entropia como:
(12) 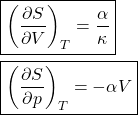
Pressão Interna
A pressão interna (![]() ) também pode ser obtida de propriedade mensuráveis:
) também pode ser obtida de propriedade mensuráveis:
Da equação de Gibbs para ![]() :
:
![]()
Dividindo por ![]() , mantendo
, mantendo ![]() fixo:
fixo:
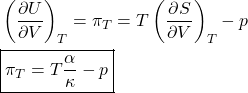
Para gases perfeitos:
![]()
![]()
Como se espera para um gás perfeito.
Dependência de 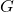 com
com 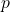 e
e 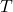
Sem dúvida a relação mais importante desta aula é a dependência de ![]() com a pressão e a temperatura. Das relações obtidas:
com a pressão e a temperatura. Das relações obtidas:
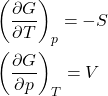
A primeira dessas relações indica que ![]() sempre cai com a temperatura (afinal
sempre cai com a temperatura (afinal ![]() ) e, ainda, que essa queda é maior para gases do que para líquidos e sólidos (já que
) e, ainda, que essa queda é maior para gases do que para líquidos e sólidos (já que ![]() . O gráfico abaixo ilustra a queda de
. O gráfico abaixo ilustra a queda de ![]() com
com ![]() para os três estados de uma mesma substância. Repare que o cruzamento das curvas representa o equilíbrio entre as fases, ou seja, ocorrem na temperatura de fusão e ebulição.
para os três estados de uma mesma substância. Repare que o cruzamento das curvas representa o equilíbrio entre as fases, ou seja, ocorrem na temperatura de fusão e ebulição.
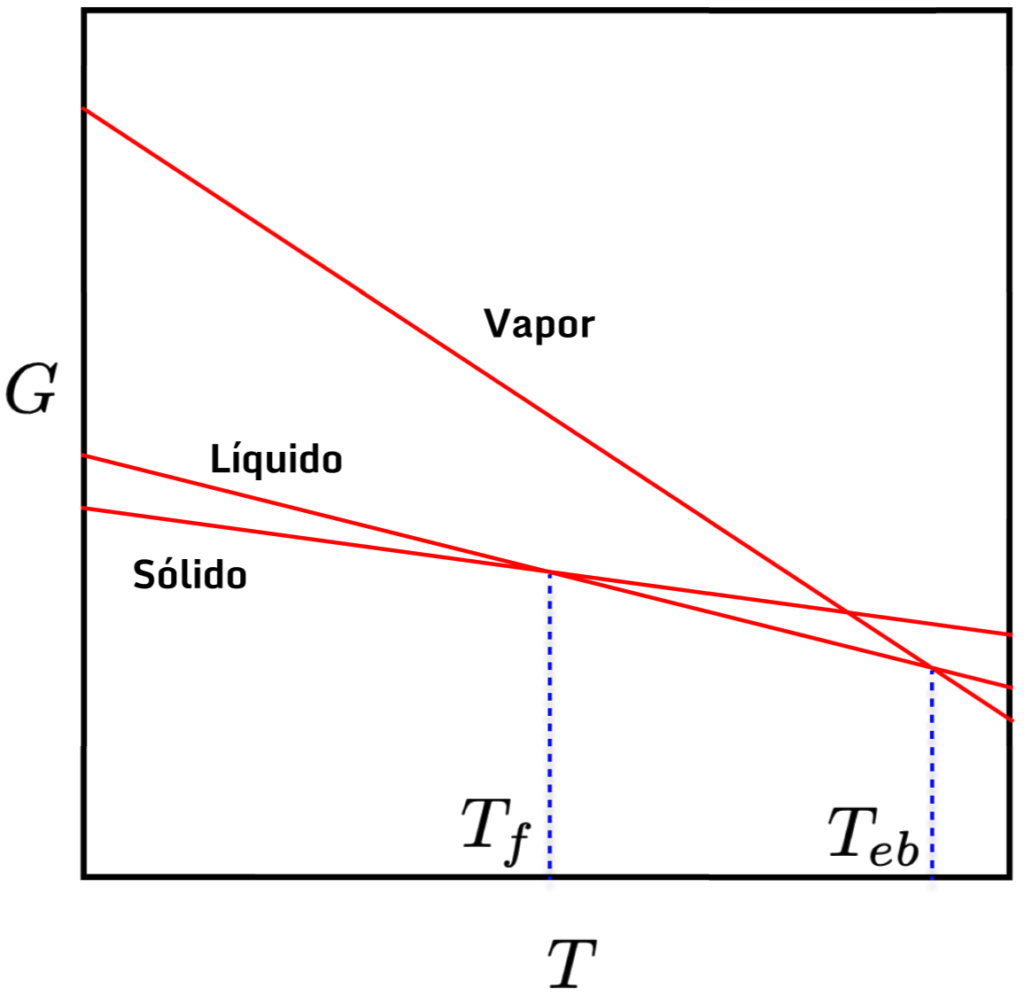
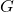 com
com  para os estados de agregação.
para os estados de agregação.A dependência de ![]() com
com ![]() também é importante e será usada na descrição de termodinâmica de misturas, envolvendo o contexto do potencial químico. Por hora, vale a pena citar apenas que a segunda relação obtida mostra que
também é importante e será usada na descrição de termodinâmica de misturas, envolvendo o contexto do potencial químico. Por hora, vale a pena citar apenas que a segunda relação obtida mostra que ![]() sempre cresce com
sempre cresce com ![]() e que esse crescimento é muito mais pronunciado para gases, uma vez que o volume de gases é sempre maior do que de líquidos e sólidos de uma substância. O gráfico abaixo mostra essa dependência.
e que esse crescimento é muito mais pronunciado para gases, uma vez que o volume de gases é sempre maior do que de líquidos e sólidos de uma substância. O gráfico abaixo mostra essa dependência.
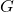 com
com 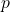 para os estados de agregação.
para os estados de agregação.Exercícios
1) Encontre a dependência isotérmica da entropia com o volume:
![]()
Para:
a) o gás ideal,
b) o gás de van der Waals
c) o gás de Dieterici.
Gabarito
a)
![]()
b)
![]()
c)
![]()
Resolução
2) Considere a dependência da entropia com a temperatura e com a pressão:
![]()
Usando a definição de
![]()
Resolução
3) Encontre a expressão matemática que permita relacionar o valor de ![]() de um gás ideal em duas pressões diferentes:
de um gás ideal em duas pressões diferentes: ![]() e
e ![]() .
.
Gabarito
![]()
Resolução
4) Repita a questão 3 para um gás de van der Waals (despreze as interações atrativas, fazendo ![]() e
e ![]() ).
).
Gabarito
![]()
