1) Calcule a variação de entropia sofrida por 
de gás argônio, quando são aquecidos isobaricamente de 
até 
em duas situações distintas:
a) Considerando o comportamento de gás monoatômico ideal.
b) Considerando que o 
do gás varia na faixa de temperaturas indicada de acordo com a função:
Gabarito
a) 
b) 
2) Um mol de um gás ideal é expandido isotermicamente a 
até que seu volume seja triplicado.
Encontre os valores de 
, 
e 
nas seguintes condições:
a) A expansão é realizada reversivelmente.
b) A expansão é realizada irreversivelmente onde 
de calor é menos absorvido do que em (a).
c) A expansão é livre.
Gabarito
a) 
e 
b) 
, 
e 
c) , 
e
3) Calcule a variação de entropia do seguinte processo a 
:
Sabendo que a entalpia de vaporização da água é
.
Gabarito
4) Foi sugerido que α-cianopiridina pode ser preparada a partir de cianogênio e butadieno pela reação: 
Considerando os dados termodinâmicos fornecidos abaixo, você consideraria válido tentar realizar esta reação em laboratório?
| Molécula |  |  |
| Butadieno (g) |  |  |
| Cianogênio (g) |  |  |
 -cianopiridina (g) |  |  |
 |  |  |
Gabarito
, logo é válido tentar realizar a reação em laboratório nas condições citadas.
5) Para a reação:
e 
Estime o valor de 
se 
for considerado independente da temperatura.
Gabarito
6) Um mol de vapor é condensado reversivelmente para água líquida a e pressão de 
. O calor de vaporização da água é 
. Assumindo que o vapor se comporta como um gás ideal, calcule 
, 
, 
, 
, 
e 
para o processo de condensação.
Gabarito
7) Sabendo que 
, 
, 
e 
, prove as relações de Maxwell:
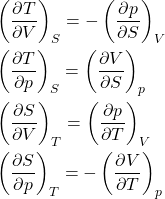
Gabarito
A demonstração foi feita em aula. Tentem sem olhar o caderno.
8) Para a reação:
é 
a 
. Se uma mistura inicial contendo 
de 
e 
de 
(inerte) é passada sobre um catalisador de desidrogenação a , qual é a composição percentual de equilíbrio da mistura gasosa efluente?
A pressão total é mantida em 
. Dado: 
a 
.
Calcule 
a . (Assuma 
)
Gabarito
A demonstração foi feita em aula. Tentem sem olhar o caderno.
9) Para a dissociação do gás sulfeto de di-hidrogênio:
A constante de equilíbrio
é 
a 
e a entalpia de dissociação 
é 
. a) Encontre a constante de equilíbrio padrão da reação a
.b) Como o aumento na pressão afeta o equilíbrio?
c) Como a adição de um gás inerte na mistura reacional afeta o equilíbrio?
d) Como o aquecimento afeta o equilíbrio?
Gabarito
a) 
b) O aumento da pressão por variação isotérmica de volume irá deslocar o equilíbrio no sentido de favorecer a formação de 
.
c) A adição de gás inerte não afeta o equilíbrio.
d) Como a reação direta é endotérmica, o aquecimento aumenta a constante de equilíbrio, de modo que o aquecimento leva a um novo estado de equilíbrio, com composição mais rica em produtos do que o original.