Até o momento, maior parte dos tópicos abordados até aqui tratam de sistemas em equilíbrio, de modo que, ao longo do tempo, nenhuma mudança macroscópica parece ocorrer depois que esse estado é atingido. Como químico, você deve lembrar que uma reação química pode avançar espontaneamente até que o mínimo de ![]() seja atingido e, a partir de então, nenhuma reação parece ocorrer. O mesmo ocorre com outros tipos de equilíbrio. Obviamente, mesmo em equilíbrio, é possível provocar mudanças em um sistema, de modo que todos os estados intermediários visitados ao longo dessa mudança são, também, estados de equilíbrio.
seja atingido e, a partir de então, nenhuma reação parece ocorrer. O mesmo ocorre com outros tipos de equilíbrio. Obviamente, mesmo em equilíbrio, é possível provocar mudanças em um sistema, de modo que todos os estados intermediários visitados ao longo dessa mudança são, também, estados de equilíbrio.
Antes de atingir o equilíbrio (mecânico, térmico, de fases, químico, …), o descritor termodinâmico adequado ainda não atingiu seu valor mínimo. Se ![]() e
e ![]() forem constantes, por exemplo,
forem constantes, por exemplo, ![]() ainda não é mínimo antes do equilíbrio. Se estivermos falando de uma mudança de fase, transporte de matéria ocorrerá até que o sistema tenha o mínimo de
ainda não é mínimo antes do equilíbrio. Se estivermos falando de uma mudança de fase, transporte de matéria ocorrerá até que o sistema tenha o mínimo de ![]() alcançado e o equilíbrio de fases estarám, então, estabelecido (quando os potenciais químicos são idênticos).
alcançado e o equilíbrio de fases estarám, então, estabelecido (quando os potenciais químicos são idênticos).
Neste tópico, veremos as leis básicas que descrevem fenômenos de transferência, que ocorrem comumente em sistemas que ainda não estão em equilíbrio e, logo, não fazem parte da termodinâmica clássica. Dessa forma, uma variável nova surgirá: o tempo; de modo que os fenômenos de transporte é um tópico, na realidade, da cinética física.
Existem muitos tipos de transporte: de calor, de matéria, de carga, de momento, etc. No entando, todos eles parecem compartilhar de uma característica em comum: dependem do gradiente de alguma propriedade que dirige essa transferência, ou seja, como ela varia no espaço, em uma direção específica.
Químicos precisam entender como cargas são transportadas em células eletroquímicas; como o soluto é transportado pelo solvente ao se dissolver nele; como calor é transportado em um sistema de aquecimento. Além disso, outras áreas da ciência se beneficiam desse conhecimento. Biólogos, por exemplo, precisam entender como são transportadas diversas espécies químicas para dentro e para fora de uma célula, através de suas membranas plasmáticas. Neurologistas precisam compreender como impulsos nervosos são transportados pelo corpo humano. Enfermeiros precisam compreender como o sangue é transportado nas nossas veias e artérias. A indústria petroquímica precisa descrever bem o movimento de fluidos como petróleo, seus derivados líquidos e gases em seus dutos.
Transporte de Calor
Imagine duas placas metálicas com temperaturas diferentes ![]() , em contato com uma substância (água, como mostra o exemplo da próxima figura). O sistema evoluirá espontaneamente até obedecer à lei zero da termodinâmica, ou seja, até que as temperaturas dos três corpos sejam idênticas.
, em contato com uma substância (água, como mostra o exemplo da próxima figura). O sistema evoluirá espontaneamente até obedecer à lei zero da termodinâmica, ou seja, até que as temperaturas dos três corpos sejam idênticas.
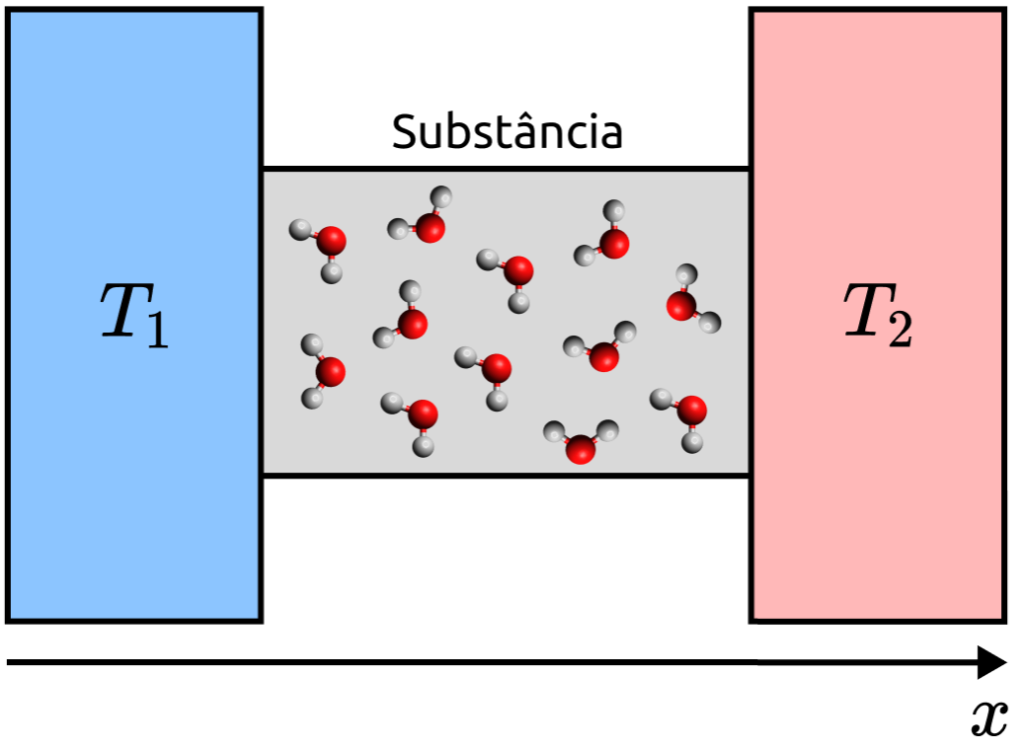
Estamos preocupados em descrever a capacidade que o material intermediário tem de conduzir calor. A quantidade de energia transportada ![]() deve depender de algumas propriedades intuitivas. Uma delas é o tempo (
deve depender de algumas propriedades intuitivas. Uma delas é o tempo (![]() ), ou seja, quanto mais tempo observamos a transferência ocorrer, mais calor será transportado. Outra seria a área da seção transversão (
), ou seja, quanto mais tempo observamos a transferência ocorrer, mais calor será transportado. Outra seria a área da seção transversão (![]() ), no sentido que, se uma maior área de contato com as placas for disponibilizada, mais calor será transportado. Além disso, poderíamos imaginar que a quantidade de calor dependa da diferença de temperatura entre as placas (
), no sentido que, se uma maior área de contato com as placas for disponibilizada, mais calor será transportado. Além disso, poderíamos imaginar que a quantidade de calor dependa da diferença de temperatura entre as placas (![]() ), no sentido de que, quanto maior a diferença de temperatura, maior será a quantidade de calor transportada. Além disso, a quantidade de calor deve depender da largura que separa as placas (
), no sentido de que, quanto maior a diferença de temperatura, maior será a quantidade de calor transportada. Além disso, a quantidade de calor deve depender da largura que separa as placas (![]() ), no sentido que maior será a transferência de calor para larguras pequenas.
), no sentido que maior será a transferência de calor para larguras pequenas.
Obviamente todas essas discussões são apenas qualitativas e ainda não chegamos a uma expressão matemática para o processo. A primeira tentativa a ser feita é apostar na sorte de que a dependência do calor com todas essas propriedades seja linear, ou seja, das suas primeiras potências. Assim:
![]()
O ser humano foi agraciado com o fato da observação experimental obedecer exatamente a esta proporcionalidade. Faltam duas coisas nesta expressão: a constante de proporcionalidade, que chamaremos de ![]() e um sinal negativo. Esta constante é chamada de condutividade térmica e o sinal de menos se faz necessário porque o sentido do transporte de calor é oposto ao sentido positivo do eixo
e um sinal negativo. Esta constante é chamada de condutividade térmica e o sinal de menos se faz necessário porque o sentido do transporte de calor é oposto ao sentido positivo do eixo ![]() . Ao incluir esses detalhes, obtemos:
. Ao incluir esses detalhes, obtemos:
![]()
Porém, uma abordagem mais rigorosa consiste em dividir a substância em pequenos volumes de área de base ![]() e altura
e altura ![]() , como mostra a figura abaixo.
, como mostra a figura abaixo.
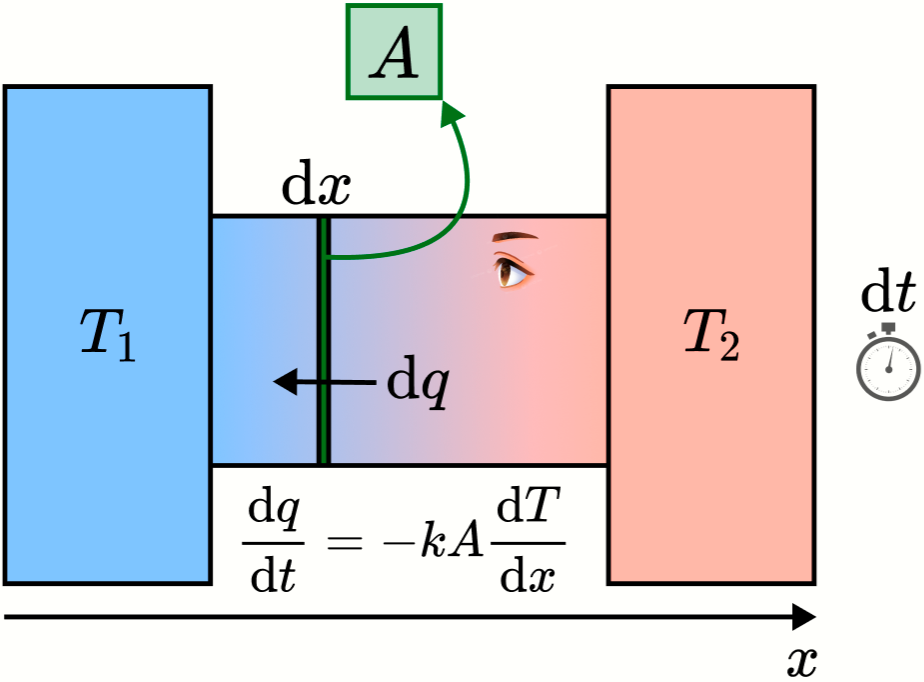
E a expressão se torna:
![]()
Porém, podemos escrever a expressão de forma que apareçam duas grandezas importantes: o gradiente de temperatura (![]() ) e a potência, isto é, a razão
) e a potência, isto é, a razão ![]() , como mostrado abaixo:
, como mostrado abaixo:
![]()
Esta é a lei de Fourier da condução de calor. Vamos analisar a condutividade térmica. Antes de mais nada é importante dizer que ela é única de cada material. Para gases, ![]() assume valores muito baixos, pois o mecanismo de condução envolve interações entre partículas, colisões e vibrações. A condutividade térmica de materiais em suas fases condensadas é consideravelmente maior, porque líquidos e sólidos permitem que as partículas transfiram energia umas para as outras com muito mais facilidade do que em gases. Em sólidos, certamente, a condutividade térmica é maior, sendo ainda mais expressiva quando o sólido é condutor elétrico (como o cobre, por exemplo), uma vez que a movimentação dos elétrons no metal facilita a transferência de energia. Na figura abaixo estão os valores das condutividades de alguns materiais:
assume valores muito baixos, pois o mecanismo de condução envolve interações entre partículas, colisões e vibrações. A condutividade térmica de materiais em suas fases condensadas é consideravelmente maior, porque líquidos e sólidos permitem que as partículas transfiram energia umas para as outras com muito mais facilidade do que em gases. Em sólidos, certamente, a condutividade térmica é maior, sendo ainda mais expressiva quando o sólido é condutor elétrico (como o cobre, por exemplo), uma vez que a movimentação dos elétrons no metal facilita a transferência de energia. Na figura abaixo estão os valores das condutividades de alguns materiais:

Repare na unidade de ![]() , no sistema internacional:
, no sistema internacional:
![Rendered by QuickLaTeX.com \begin{align*}&\dv{q}{t} = -\kappa_T A \dv{T}{x}\\&\kappa_T = -\f{\dd{q}\dd{x}}{A\dd{t}\dd{T}}\\&[\kappa_T] = \f{\mathrm{J ~ m}}{\mathrm{m^2 ~ s ~ K}} = \boxed{\mathrm{W~m^{-1}~K^{-1}}}\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-4f39631525a4cd5b0cfa133880028c02_l3.png)
Transferência de Momento
Líquidos e gases são fases fluidas, ou seja, migram de uma região de maior pressão para outra de menor pressão. No entanto, nem todos os líquidos fluem com mesma velocidade. Sob a mesma diferença de pressão, a água flui muito mais rapidamente do que o mel. A lentidão do mel se deve a uma propriedade de todos os fluidos, associada à resistência ao movimento, chamada de viscosidade. Veremos que essa resistência é resultado de um fenômeno de transporte (e não é o transporte de matéria, ou seja, do líquido em si).
Para descrever a viscosidade, consideremos um fluido (água, por exemplo) que está em repouso entre duas superfícies: a inferior (fixa) e a superior (móvel), como mostra a figura abaixo.
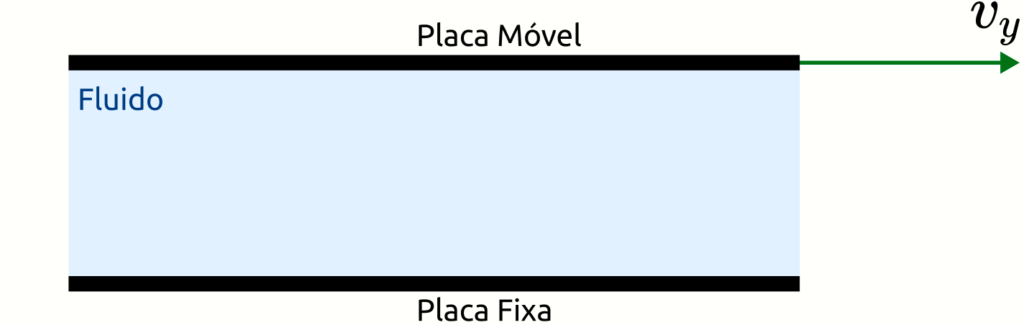
Como as moléculas do fluido estão em contato direto com as placas, interações entre as moléculas do fluido e as superfícies das placas são responsáveis por:
- Fazer a camada de líquido mais próxima à placa móvel se movimentar na mesma velocidade que a dela.
- Fazer a camada de líquido mais próxima à placa fixa ficar em repouso (mesma velocidade que ela).
A força que a placa móvel exerce sobre a camada superior de líquido é chamada de força de cisalhamento (![]() ), pois ocorre paralela à superfície do líquido. Divida pela área da superfície de aplicação dessa força, obtemos a tensão de cisalhamento
), pois ocorre paralela à superfície do líquido. Divida pela área da superfície de aplicação dessa força, obtemos a tensão de cisalhamento ![]() . Repare que dividimos força por área e não chamamos de pressão, porque essa força não é perpendicular à superfície, mas paralela a ela.
. Repare que dividimos força por área e não chamamos de pressão, porque essa força não é perpendicular à superfície, mas paralela a ela.

Como resultado deste comportamento, é natural que surja um gradiente de velocidades no interior do líquido, representado de forma dupla na figura abaixo, ou seja, como uma sequência de vetores e um espectro de cores que representa a velocidade ![]() do líquido (quanto mais próximo for do vermelho, mais rápida é a camada de fluido.
do líquido (quanto mais próximo for do vermelho, mais rápida é a camada de fluido.

Observe que o líquido se movimenta na direção ![]() , mas o gradiente de velocidades ocorre na direção perpendicular
, mas o gradiente de velocidades ocorre na direção perpendicular ![]() . As moléculas de uma determinada camada podem interagir com as de outra camada, mais acima e, logo, mais rápida. Nessa interação, as moléculas da camada rápida aceleram as da camada lenta, transferindo-lhes momento (
. As moléculas de uma determinada camada podem interagir com as de outra camada, mais acima e, logo, mais rápida. Nessa interação, as moléculas da camada rápida aceleram as da camada lenta, transferindo-lhes momento (![]() ) e, pela terceira lei de Newton, as moléculas da camada lenta desaceleram as da camada rápida. Perceba que o gradiente de velocidades provocou um atrito interno, responsável pela viscosidade.
) e, pela terceira lei de Newton, as moléculas da camada lenta desaceleram as da camada rápida. Perceba que o gradiente de velocidades provocou um atrito interno, responsável pela viscosidade.
De forma semelhante ao que foi feito para a condução de calor, a quantidade de momento ![]() que é transferida entre as camadas é diretamente proporcional à área
que é transferida entre as camadas é diretamente proporcional à área ![]() de contato entre elas, à diferença de velocidade
de contato entre elas, à diferença de velocidade ![]() e ao tempo de contato
e ao tempo de contato ![]() ; além disso,
; além disso, ![]() deve ser inversamente proporcional à separação
deve ser inversamente proporcional à separação ![]() entre as camadas. Assim:
entre as camadas. Assim:
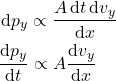
Perceba que, naturalmente, surgiu o gradiente de velocidades ![]() do lado direito. A constante de proporcionalidade dessa relação é chamada de coeficiente de viscosidade
do lado direito. A constante de proporcionalidade dessa relação é chamada de coeficiente de viscosidade ![]() . Pelo fato do momento ser transferido da camada rápida para a lenta, o sentido de transferência de momento é o oposto ao crescimento de
. Pelo fato do momento ser transferido da camada rápida para a lenta, o sentido de transferência de momento é o oposto ao crescimento de ![]() ; isso cria a necessidade de um sinal de menos, análogo ao presente na lei de Fourier. Assim, poremos escrever a lei de Newton para a viscosidade.
; isso cria a necessidade de um sinal de menos, análogo ao presente na lei de Fourier. Assim, poremos escrever a lei de Newton para a viscosidade.
![]()
Desde que a velocidade de escoamento não seja muito alta, a lei de Newton para a viscosidade é bem obedecida. Para tais situações, chamamos o material de um fluido newtoniano e o movimento em si como um fluxo laminar ou viscoso. Em altas velocidades, moléculas de uma camada podem invadir outras camadas e a organização laminar se perde por inteiro, de forma que a lei de Newton não é mais obedecida. Chamamos o material com esse comportamento de um fluido não newtoniano e seu movimento é um fluxo turbulento.
A unidade de ![]() no SI é:
no SI é:
![]()
É comum trabalharmos com a unidade poise (![]() ), onde
), onde ![]() . Isso nos permite escrever duas relações úteis:
. Isso nos permite escrever duas relações úteis: ![]() e
e ![]() .
.
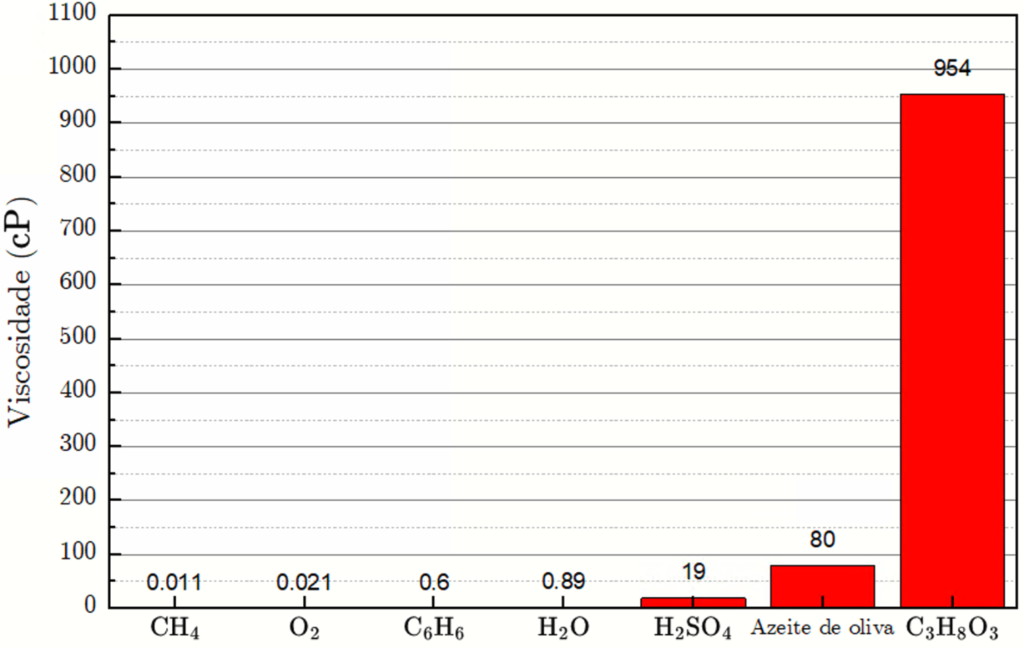
Como a transferência de momento envolve interações intermoleculares, existe uma tendência que líquidos com interações intermoleculares mais intensas sejam mais viscosos. O gráfico a seguir mostra a variação de ![]() para diferentes líquidos. Perceba que a viscosidade dos gases é muito pequena (fluem com muito facilidade). Além disso, a viscosidade do benzeno é menor do que a da água, uma vez que o atrito interno na água é maior, devido às fortes ligações de hidrogênio no líquido.
para diferentes líquidos. Perceba que a viscosidade dos gases é muito pequena (fluem com muito facilidade). Além disso, a viscosidade do benzeno é menor do que a da água, uma vez que o atrito interno na água é maior, devido às fortes ligações de hidrogênio no líquido. ![]() apresenta interações ainda mais fortes do que a água, justificando a maior viscosidade. Azeite de oliva é composto por moléculas de menor polaridade, mas não se engane achando que moléculas apolares necessariamente interage menos do que moléculas polares, como água. Se a polarizabilidade da molécula apolar for elevada, as forças dispersivas podem superar ligações de hidrogênio. Esta é a razão do ponto de ebulição normal do heptano ser muito próximo ao da água. As interações dispersivas muito intensas no azeite explicam sua alta viscosidade e as ligações de hidrogênio numerosas e intensas no glicerol são as responsáveis por ele ser o líquido mais viscoso dentre os mostrados no gráfico.
apresenta interações ainda mais fortes do que a água, justificando a maior viscosidade. Azeite de oliva é composto por moléculas de menor polaridade, mas não se engane achando que moléculas apolares necessariamente interage menos do que moléculas polares, como água. Se a polarizabilidade da molécula apolar for elevada, as forças dispersivas podem superar ligações de hidrogênio. Esta é a razão do ponto de ebulição normal do heptano ser muito próximo ao da água. As interações dispersivas muito intensas no azeite explicam sua alta viscosidade e as ligações de hidrogênio numerosas e intensas no glicerol são as responsáveis por ele ser o líquido mais viscoso dentre os mostrados no gráfico.
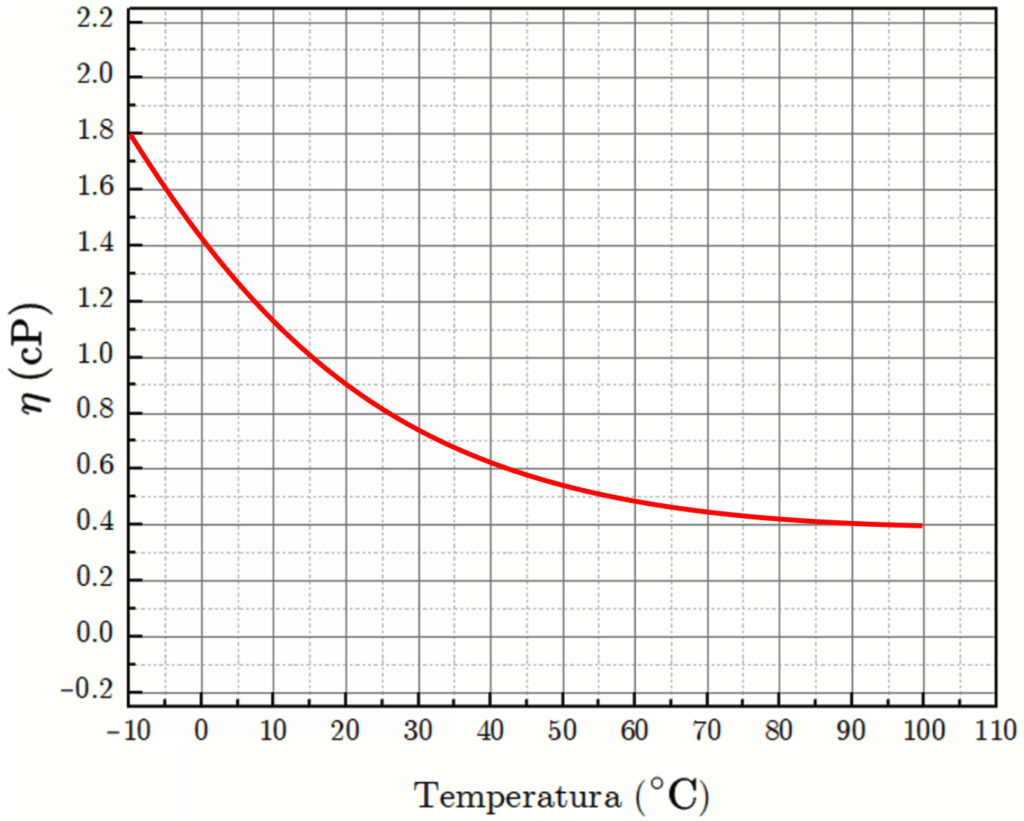
É conhecido que o aquecimento enfraquece interações intermoleculares. Esse enfraquecimento desfavorece a transferência de momento entre as camadas com diferentes velocidades, de modo que a viscosidade de líquidos diminui com a temperatura, como mostra o gráfico abaixo, para a água.
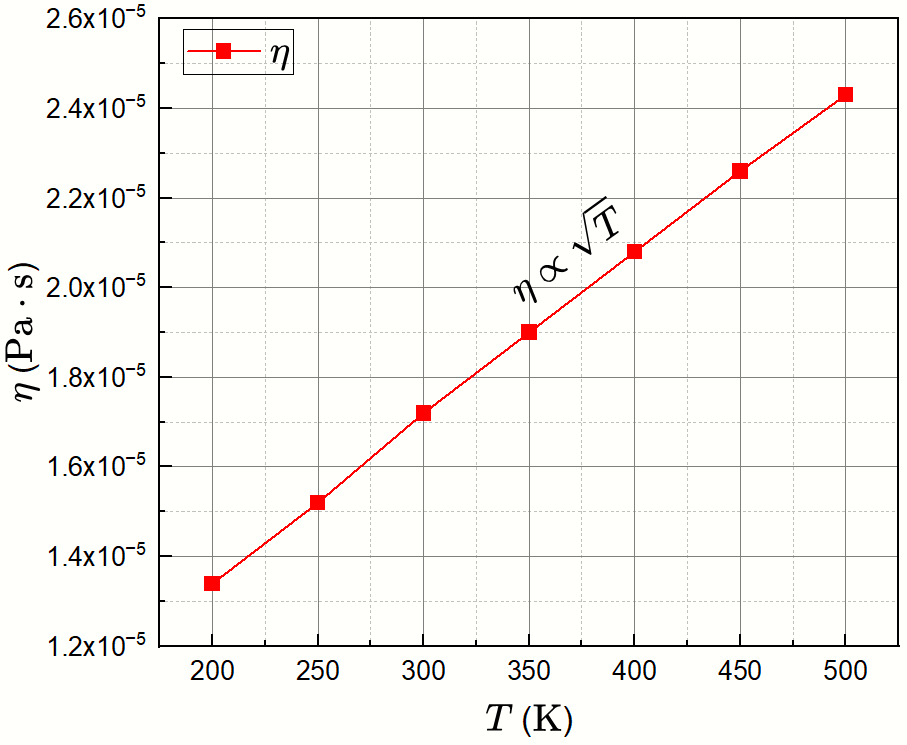
Para gases, o momento é trocado de maneira diferente. Como as interações intermoleculares nos gases são pouco intensas, a troca de momento ocorre pelo tipo de interação mais importante nessa fase da matéria: as colisões. Enquanto nos líquidos a troca de momento ocorre pela interação entre moléculas de camadas diferentes, sem, efetivamente, moléculas saírem de suas próprias camadas, nos gases, as colisões são as responsáveis pelo atrito interno. Assim, espera-se que, pelo fato do aumento da temperatura aumentar o número de colisões, a viscosidade de gases aumente com a temperatura.
Apesar de não ser explorado aqui, é possível provar (usando teoria cinética dos gases) que a viscosidade de gases aumenta com ![]() (a função
(a função ![]() é uma função crescente bem suave, parecendo uma reta para altos valores de
é uma função crescente bem suave, parecendo uma reta para altos valores de ![]() ). Os dados experimentais para o argônio gasoso são mostrados abaixo:
). Os dados experimentais para o argônio gasoso são mostrados abaixo:
O físico e médico francês Jean Léonard Marie Poiseuille (1797–1869) preocupava-se com a mecânica dos fluidos no século XIX, em especial o sangue, mas seu trabalho abrange toda a física. Ele estudou o fluxo de fluidos em tubos (como ocorre com o sangue em nossas veias e artérias), devido a uma diferença de pressão. As observações de Poiseuille mostraram que a vazão (![]() , volume de fluido por unidade de tempo) é:
, volume de fluido por unidade de tempo) é:
- diretamente proporcional à diferença de pressão que causa o fluxo:
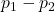 .
. - diretamente proporcional à quarta potência do raio da tubulação:
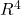 .
. - Inversamente proporcional ao comprimeno do tubo:
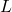 .
. - Inversamente proporcional à viscosidade do fluido:
 .
.
Mais especificamente a lei de Poiseuille é dada pela equação 1.
(1) 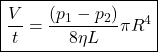
A análise dimensional do lado direito da igualdade nos permite chegar à:
![]()
Como e esperado para uma vazão.
A medida da viscosidade é feita pela medida do tempo necessário para algum fenômeno no fluido ocorrer. Uma dessas estratégias é o uso do viscosímetro de Ostwald, que é um tubo em U, onde o fluido é inserido e, por diferença de pressão, é obrigado a atravessar uma região de volume conhecido. Mede-se o tempo necessário para que o líquido percorra essa região. Quanto mais viscoso for o líquido, maior será o tempo medido. Um esboço de um viscosímetro de Ostwald é mostrado na figura abaixo.

Na prática, o que é medido é a viscosidade relativa. Usando dois líquidos (![]() e
e ![]() ), a aplicação da lei de Poiseuille nos permite escrever:
), a aplicação da lei de Poiseuille nos permite escrever:
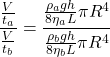
Como ![]() ,
, ![]() ,
, ![]() e
e ![]() são os mesmos para os movimentos dos dois líquidos:
são os mesmos para os movimentos dos dois líquidos:
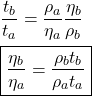
Exercícios
1) A ![]() , água pura com viscosidade absoluta de
, água pura com viscosidade absoluta de ![]() requer
requer ![]() para fluir através do capilar de um viscosímetro de Ostwald. A
para fluir através do capilar de um viscosímetro de Ostwald. A ![]() , o tolueno requer
, o tolueno requer ![]() . Se as densidades da água e do tolueno são
. Se as densidades da água e do tolueno são ![]() e
e ![]() respectivamente, calcule a viscosidade do tolueno.
respectivamente, calcule a viscosidade do tolueno.
Gabarito
![]()
Resolução
2) Calcule a viscosidade de um líquido que escoa através de um tubo com raio de ![]() e comprimento de
e comprimento de ![]() . A diferença de pressão entre as extremidades do tubo é de
. A diferença de pressão entre as extremidades do tubo é de ![]() , e a vazão volumétrica é de
, e a vazão volumétrica é de ![]() .
.
Gabarito
![]()
Resolução
3) Considere água fluindo com viscosidade ![]() em temperatura ambiente no interior de um tubo de diâmetro
em temperatura ambiente no interior de um tubo de diâmetro ![]() e calcule o valor máximo de sua velocidade de escoamento para que o fluido se mantenha laminar.
e calcule o valor máximo de sua velocidade de escoamento para que o fluido se mantenha laminar.
Gabarito
![]()
Resolução
4) Considere que acetona líquida esteja fluindo em um tubo de vidro a ![]() . Ao aquecer o líquido, a viscosidade cai em
. Ao aquecer o líquido, a viscosidade cai em ![]() . Sabendo que a energia das interações dipolo-dipolo é de
. Sabendo que a energia das interações dipolo-dipolo é de ![]() , calcule a temperatura final da acetona.
, calcule a temperatura final da acetona.
Gabarito
![]()
Resolução
5) Suponha que ![]() de uma solução com concentração de um glicídio igual a
de uma solução com concentração de um glicídio igual a ![]() esteja em contato com
esteja em contato com ![]() de solução
de solução ![]() do mesmo glicídio,
do mesmo glicídio, ![]() à direita, mas separadas por uma parede. Ao remover a barreira, ocorre difusão com fluxo
à direita, mas separadas por uma parede. Ao remover a barreira, ocorre difusão com fluxo ![]() . Qual é o coeficiente de difusão na solução?
. Qual é o coeficiente de difusão na solução?
Gabarito
![]()
Resolução
6) Ao passar o dia na praia, uma família deixou o carro exposto ao intenso calor do verão carioca. A temperatura inicial no interior do carro (quando a família chega ao local e desliga o ar condicionado) é de ![]() e, no exterior do veículo,
e, no exterior do veículo, ![]() . O parabrisa do carro possui dimensões de
. O parabrisa do carro possui dimensões de ![]() e é feito de um tipo de vidro com condutividade térmica
e é feito de um tipo de vidro com condutividade térmica ![]() . Calcule a quantidade de calor que flui para dentro do veículo por segundo quando a família deixa o carro.
. Calcule a quantidade de calor que flui para dentro do veículo por segundo quando a família deixa o carro.
Gabarito
![]()
Resolução
7) Em um dia muito frio, a temperatura interna de uma sala é mantida constante a ![]() , enquanto que a temperatura externa é de apenas
, enquanto que a temperatura externa é de apenas ![]() . A sala possui uma janela de
. A sala possui uma janela de ![]() de altura por
de altura por ![]() de comprimento. Suponha que o vidro da janela tenha a mesma condutividade térmica do vidro da questão anterior e tem
de comprimento. Suponha que o vidro da janela tenha a mesma condutividade térmica do vidro da questão anterior e tem ![]() de espessura. Que quantidade de calor é perdida para o ambiente durante um intervalo de
de espessura. Que quantidade de calor é perdida para o ambiente durante um intervalo de ![]() ?
?
Gabarito
![]()
Resolução
8) Explique o mecanismo de transferência de momento em líquidos e gases como fluidos reais (com viscosidade).
Gabarito
Para líquidos, as camadas mais próximas à parede móvel serão compostas por moléculas mais rápidas. Essas moléculas interagem com moléculas da camada imediatamente inferior e com velocidades menores. Essa interação ocasiona transporte de momento e, como consequência, atrito interno. Quanto maior é a intensidade da troca de momento maior é o coeficiente de viscosidade ![]() . É importante enfatizar que a troca de momento ocorre sem que as moléculas saiam de suas camadas. Se isso ocorrer, o fluxo deixa de ser laminar e passa a ser turbulento.
. É importante enfatizar que a troca de momento ocorre sem que as moléculas saiam de suas camadas. Se isso ocorrer, o fluxo deixa de ser laminar e passa a ser turbulento.
Para gases, as moléculas certamente sairão de suas camadas originais. O estado gasoso é caótico e, quando há fluxo de gás, o atrito interno que vem das forças intermoleculares é desprezível, pois as interações são pouco intensas. A viscosidade de gases surge da troca de momento provocada nas colisões.
