Equilíbrio Químico

Potenciais Químicos em Misturas de Gases Perfeitos

Considere a reação representada pela seguinte equação:

$\begin{align*} \ce{aA(g) + bB(g) \rightleftharpoons cC(g) + dD(g)}\end{align*}$

A condição de equilíbrio é estabelecida pela igualdade dos potenciais químicos, ou seja:

$\begin{align*} a\mu_\mathrm{A} + b\mu_\mathrm{B} = c\mu_\mathrm{C} + d\mu_\mathrm{D}\end{align*}$

Ou, escrita de outra forma:

$\begin{align*} -a\mu_\mathrm{A} - b\mu_\mathrm{B} + c\mu_\mathrm{C} + d\mu_\mathrm{D} = 0\end{align*}$

Essa expressão fica escrita de forma mais concisa, considerando que $-a$ , $-b$ , $+c$ e $+d$ são os números estequiométricos dos participantes. Assim:

$\begin{align*} \sum_i{\nu_i \mu_i} = 0\end{align*}$

Como vimos anteriormente, o potencial químico de um gás ideal em uma mistura de gases ideais pode ser escrito como segue:

$\begin{align*} \mu_i = \mu_i^\circ + RT\ln{\f{p_i}{p^\circ}}\end{align*}$

E, ao substituir na expressão que obtivemos:

$\begin{align*} \sum_i{\nu_i \parentesis{\mu_i^\circ + RT\ln{\f{p_i}{p^\circ}}}} = 0\end{align*}$

Aplicando a distributiva:

$\begin{align*} \sum_i{\parentesis{\nu_i\mu_i^\circ + \nu_iRT\ln{\f{p_i}{p^\circ}}}} = 0\end{align*}$

Separando em duas somas:

$\begin{align*} \sum_i{\parentesis{\nu_i\mu_i^\circ}} + \sum_i{\parentesis{\nu_iRT\ln{\f{p_i}{p^\circ}}}} = 0\end{align*}$

O primeiro termo é simplesmente a energia livre de Gibbs molar de reação ( $\Delta_rG_m^\circ$ ) e vamos fatorar $R$ e $T$ no segundo termo:

$\begin{align*} \Delta_rG_m^\circ + RT\sum_i{\parentesis{\nu_i\ln{\f{p_i}{p^\circ}}}} = 0\end{align*}$

Aplicando a propriedade abaixo:

$\begin{align*} b\ln{a} = \ln{a^b}\end{align*}$

Podemos escrever:

$\begin{align*} \Delta_rG_m^\circ + RT\sum_i{\ln{\parentesis{\f{p_i}{p^\circ}}^{\nu_i}}} = 0\end{align*}$

Aplicando a outra propriedade de logaritmos mostrada abaixo:

$\begin{align*} \ln{a} + \ln{b} = \ln{ab}\end{align*}$

Podemos escrever:

$\begin{align*} \Delta_rG_m^\circ + RT\ln{\colchetes{\prod_i{\parentesis{\f{p_i}{p^\circ}}^{\nu_i}}}} = 0 \\ \Delta_rG_m^\circ = -RT\ln{\colchetes{\prod_i{\parentesis{\f{p_i}{p^\circ}}^{\nu_i}}}}\end{align*}$

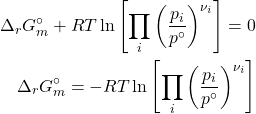
O termo do segundo membro da equação é uma grandeza nova: a constante de equilíbrio padrão da reação em função das pressões parciais.

$\begin{align*} K_p^\circ = \prod_i{\parentesis{\f{p_i}{p^\circ}}^{\nu_i}}\end{align*}$

Perceba que, como $\Delta_r G_m^\circ$ é uma grandeza medida a uma pressão fixa de $\SI{1}{\bar}$ , ela só depende da temperatura. Assim, a constante de equilíbrio também só depende da temperatura. Além disso, é importante notas que $K_p^\circ$ é adimensional, pois cada termo do produtório é uma razão entre pressões, o que nos permite cancelar as unidades. Isso é coerente com o fato de $K_p^\circ$ estar no argumento de um logaritmo.

$\begin{align*} &\Delta_rG_m^\circ = -RT\ln{K_p^\circ}\end{align*}$

Aplicado à reação citada no início desta seção:

$\begin{align*} &K_p^\circ = \parentesis{\f{p_A}{p^\circ}}^{-a}\parentesis{\f{p_B}{p^\circ}}^{-b}\parentesis{\f{p_C}{p^\circ}}^c\parentesis{\f{p_D}{p^\circ}}^d \\ &K_p^\circ = \f{\parentesis{\f{p_C}{p^\circ}}^c\parentesis{\f{p_D}{p^\circ}}^d}{\parentesis{\f{p_A}{p^\circ}}^a\parentesis{\f{p_B}{p^\circ}}^b}\end{align*}$

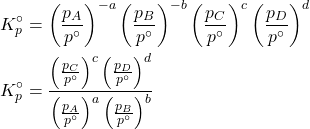
Dessa forma, quanto maior for a constante de equilíbrio, maiores serão as pressões parciais dos produtos, comparadas com as dos reagentes e o equilíbrio favorece produtos. Analogamente, se $K_p^\circ$ for pequeno, o equilíbrio favoreceria reagentes.

A Constante de Equilíbrio Padrão em Função de Concentrações Molares
A pressão parcial de um gás perfeito pode ser escrita em função da sua concentração molar de um gás na mistura:

$\begin{align*} &p_iV = n_iRT \\ &p_i = \f{n_i}{V}RT \\ &p_i = [i] RT\end{align*}$

E podemos eliminar as pressões parciais da expressões de $K_p^\circ$ , substituindo, em cada termo, a expressão acima:

$\begin{align*} K_p^\circ = \prod_i{\parentesis{\f{[i]RT}{p^\circ}}^{\nu_i}}\end{align*}$

Multiplicando e dividindo por $p^\circ$ :

$\begin{align*} K_p^\circ = \prod_i{\parentesis{\f{[i]c^\circ RT}{p^\circ c^\circ}}^{\nu_i}}\end{align*}$

Podemos escrever o produtório como o produto de outros dois, já separando convenientemente os termos:

$\begin{align*} K_p^\circ = \prod_i{\parentesis{\f{[i]}{c^\circ}}^{\nu_i}}\prod_i{\parentesis{\f{RTc^\circ}{p^\circ}}^{\nu_i}}\end{align*}$

O primeito produtório é a constante de equilíbrio padrão em função das concentrações molares:

$\begin{align*} K_c^\circ = \prod_i{\parentesis{\f{[i]}{c^\circ}}^{\nu_i}}\end{align*}$

Que também não possui unidades. Aplicada à reação citada no início deste material:

$\begin{align*} &K_c^\circ = \parentesis{\f{[A]}{c^\circ}}^{-a}\parentesis{\f{[B]}{c^\circ}}^{-b}\parentesis{\f{[C]}{c^\circ}}^{c}\parentesis{\f{[D]}{c^\circ}}^{d} \\ &K_c^\circ = \f{\parentesis{\f{[C]}{c^\circ}}^{c}\parentesis{\f{[D]}{c^\circ}}^{d}}{\parentesis{\f{[A]}{c^\circ}}^{a}\parentesis{\f{[B]}{c^\circ}}^{b}}\end{align*}$

Mais uma vez, quando o equilíbrio favorece os produtos, a constante de equilíbrio é alta e o oposto também é válido. Podemos escrever:

$\begin{align*} K_p^\circ = K_c^\circ \prod_i{\parentesis{\f{RTc^\circ}{p^\circ}}^{\nu_i}}\end{align*}$

Que, aplicada à reação que temos usado:

$\begin{align*} K_p^\circ = K_c^\circ \parentesis{\f{RTc^\circ}{p^\circ}}^{-a-b+c+d}\end{align*}$

O expoente é simplesmente o valor numérico da variação do número de mols dos gases participantes:

$\begin{align*} K_p^\circ = K_c^\circ \parentesis{\f{RTc^\circ}{p^\circ}}^{\Delta n_ \text{gás}}\end{align*}$

O Mínimo da Energia de Gibbs

Vimos que, à $p$ e $T$ coinstantes, um processo ocorre espontaneamento até que $G$ seja minimizado e, depois disso, o equilíbrio é atingido e nenhum processo (exceto os reversíveis) podem ocorrer, pois o mínimo de $G_{p,T}$ significa um máximo de $S_\text{total}$ .

Em termos de reações químicas, suponha uma reação mais simples, como a descrita pela equação genérica $A \rightleftharpoons B$ . Se uma quantidade infinitesimal $\dd{\xi}$ de $A$ se transformar espontaneamente em $B$ (visando diminuir $G_{p,T}$ ), temos que $\dd{n_A} = -\dd{\xi}$ e, por estequiometria, $\dd{n_B} = +\dd{xi}$ .

Essa grandeza $\xi$ mostra o quanto a reação avançou nesse estágio e apresenta unidade de quantidade de matéria ( $\mathrm{mol}$ ), mas cuidado, $\xi$ só passa a ser o número de mols de algum participante quando é multiplicado pelo número estequiométrico desse participante: $\dd{n_i} = \nu_i\dd{\xi}$ . Repare que, para uma extensão mensurável $\Delta \xi$ , a variação dos números de mols dos participantes é $\Delta n_A = -\Delta \xi$ e $\Delta n_B = +\Delta \xi$ . Assim, o número de mols varia, nesse stágio, de $n_A$ para $n_A - \Delta \xi$ e de $n_B$ para $n_B + \Delta \xi$ .

Quando a reação avança em $\dd{\xi}$ , a composição de todos os participantes é alterada pela multiplicação dessa quantidade pelo respectivo número estequiomético e a energia de Gibbs varia em $\dd{\xi}$ (lembre-se que $G$ depende da composição). A energia livre de Gibbs de reação é definida pela dependência de $G$ com o grau de avanço, como mostrado na equação abaixo.

$\begin{align*}\Delta_r G = \pderiv{G}{\xi}{p,T}\end{align*}$

Perceba que a definição acima indica que o símbolo $\Delta$ é uma “derivada em relação a”. Ao avançar em $\dd{\xi}$ , a mudança de $G$ pode ser calculada diretamente dos potenciais químicos:

$\begin{align*}&\dd{G} = \mu_A\dd{n_A} + \mu_B\dd{n_B}\\&\dd{G} = \mu_A(-\dd{\xi}) + \mu_B(+\dd{\xi})\\&\dd{G} = (\mu_B - \mu_A)\dd{\xi}\\&\pderiv{G}{\xi}{p,T} = \mu_B - \mu_A\\&\Delta_r G = \mu_B - \mu_A\end{align*}$

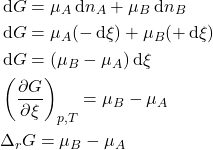
E vemos que a energia de Gibbs de reação é a diferença entre os potenciais químicos de reagentes e produtos na composição atual do sistema. Quando a composição do sistema atinge a composição de equilíbrio, $\mu_A = \mu_B$ e $\Delta_r G = 0$ , como tem que ser.

Como a composição precisa alterar-se até que $G$ seja mínimo, se traçarmos um gráfico de $G$ em função do grau de avanço $\xi$ , o mínimo ocorrerá em algum valor de $\xi$ , onde o sistema estará em equilíbrio.

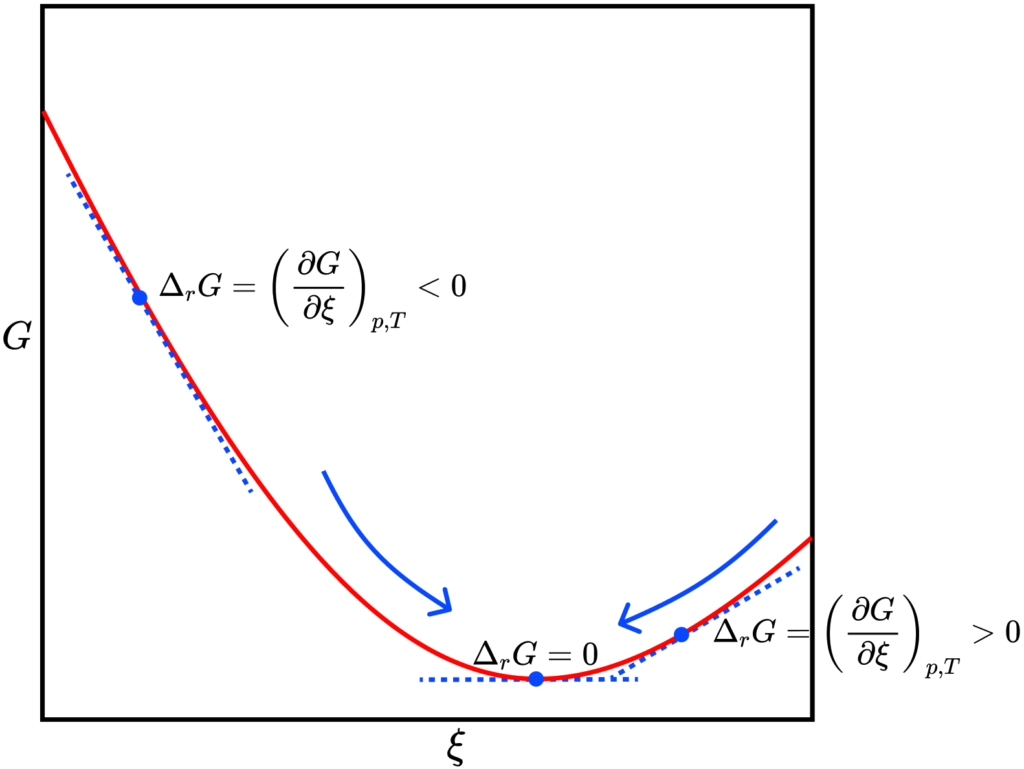
Como podemos calcular o potencial químicos dos gases em uma mistura de gases perfeitos, podemos escrever:

$\begin{align*}&\Delta_r G = (\mu_B - \mu_A) \dd{\xi}\\&\Delta_r G = (\mu_B^\circ + RT\ln{\f{p_B}{p^\circ}} - \mu_A^\circ - RT\ln{\f{p_A}{p^\circ}})\dd{\xi}\\&\Delta_r G = \Delta_r G^\circ + RT\ln{\f{p_B}{p_A}}\end{align*}$

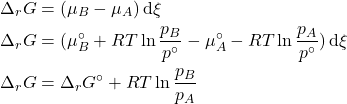
O termo no logaritmando é semelhante à já definida constante de equilíbrio, mas não é, pois as composições e as pressões parciais ainda não atingiram os valores de equilíbrio, de modo que $G_{p,T}$ ainda não é mínimo. Essa razão $p_B/p_A$ pode ser usado como um descritor, para afirmarmos se um sistema reacional atingiu ou não o equilíbrio químico. Essa razão é chamada de quociente reacional ( $Q_p^\circ$ ) e assume um valor diferente de $K_p^\circ$ enquanto $G_{p,T}$ não é totalmente minimizado.

(1) $\begin{align*}&\Delta_r G = \Delta_r G^\circ + RT\ln{Q_p^\circ} \end{align*}$

Perceba que, se $Q_p^\circ = K_p^\circ$ , o lado direito precisa ser nulo, pois $\Delta_r G^\circ = -RT\ln{K_p^\circ}$ . Se $Q_p^\circ < K_P^\circ$ , $\Delta_r G < 0$ e a reação precisa avançar para formar mais produtos para fazer $Q$ aumentar e atingir o valor de $K_p^\circ$ , minimizando $G$ . Se, por outro lado, $Q_p^\circ > K_p^\circ$ , a reação precisa “retroceder”, ou seja, transformar produtos em reagentes, diminuindo o valor de $Q_p^\circ$ até que atinja o valor de $K_p^\circ$ e $G$ seja um mínimo. Esta é a base para se compreender o deslocamento de equilíbrio quando este é perturbado devido à mudança brusca de composição (adição ou remoção de participantes).

Assim como fizemos para a constante de equilíbrio, podemos escrever o quociente reacional de maneira mais formal como:

$\begin{align*}Q_p^\circ = \prod_{i}{\parentesis{\f{p_i}{p^\circ}}}\end{align*}$

Assim como fizemos para a constante de equilíbrio, o quociente reacional pode ser escrito em função de concentrações molares.

$\begin{align*}Q_c^\circ = \prod_{i}{\parentesis{\f{[i]}{c^\circ}}}\end{align*}$

Formalizaremos todas essas formas de constantes de equilíbrio e quocientes reacionais na próxima seção.

Generalização da Constante de Equilíbrio

O desvio da idealidade para gases pode ser grande o suficiente para afetar a constante de equilíbrio e outras propriedades termodinâmicas. Soluções (apesar de não termos visto ainda) também podem apresentar desvios da idealidade. A pressão parcial de gases é corrigida levando-se em conta o coeficiente de fugacidade, que, ao ser levado em consideração na expressão de $\mu$ , obtemos o potencial químico de um gás real. Mais detalhadamente, vimos que o potencial químico de um gás ideal puro a uma pressão $p$ é:

$\begin{align*}\mu = \mu^\circ + RT\ln{\f{p}{p^\circ}}\end{align*}$

Para um gás real, usamos uma pressão efetiva ou fugacidade, que é a pressão do gás multiplicada pelo coeficiente de atividade $\varphi$ : $f = \varphi p$ . Assim, o potencial químico de um gás real, corrigido pela fugacidade, é:

$\begin{align*}&\mu = \mu^\circ + RT\ln{\f{f}{p^\circ}}\\&\text{E}\\&\mu = \mu^\circ + RT\ln{\f{\varphi p}{p^\circ}}\end{align*}$

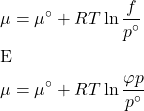
O logaritmando dessa expressão é chamado de atividade do gás:

$\begin{align*}&a = \f{\varphi p}{p^\circ}\end{align*}$

Que é uma grandeza adimensional que, para gases, tem uma função equivalente à fugacidade: corrigir propriedades termodinâmicas. Assim, o potencial químico de um gás real puro pode ser escrito como:

$\begin{align*}&\mu = \mu^\circ + RT\ln{a}\end{align*}$

O desvio da idealidade não ocorre somente em gases. Apesar de não termos visto ainda, existem soluções reais, nas quais as frações molares são substituídas pelas atividades dos participantes. A atividade de um componente de uma solução real é:

$\begin{align*}&a_i = \gamma_i x_i\end{align*}$

Repare que a atividade não é uma fração molar corrigida, mas uma fração molar efetiva, no sentido que, quando usada no lugar da fração molar nas propriedades termodinâmicas, produz dados exatos. O $\gamma_i$ simboliza o coeficiente de atividade do participante, que é uma grandeza adimensional. Podemos expressar a atividade em termos das concentrações molares, dividindo pela concentração molar padrão $c^\circ$ , para manter a adimensionalidade da atividade:

$\begin{align*}&a_i = \f{[i]}{c^\circ}\gamma_i\end{align*}$

Como $p_i$ , $[i]$ e $x_i$ figuram nas constantes de equilíbrio vistas até aqui, o uso das atividades no lugar dessas grandezas fornece valores mais exatos para a constante de equilíbrio. Assim, a constante de equilíbrio escrita em termos das atividades dos participantes, é:

$\begin{align*}&K = \prod_{i}{a_i^{\nu_i}}\end{align*}$

Por convenção, a atividade de sólidos e líquidos é igual a um ( $a = 1$ ). Assim, fica clara a razão do fato de sólidos e líquidos não serem inclusos na constante de equilíbrio. Para a reação $\mathrm{N_2(g) + 3H_2(g) \rightleftharpoons 2NH_3(g)}$ , por exemplo, podemos escrever:

$\begin{align*}&K = \f{a_\mathrm{NH_3}^2}{a_\mathrm{N_2}a_\mathrm{H_2}^3}\end{align*}$

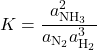
Resposta do Equilíbrio à Perturbações Externas

O equilíbrio químico pode ser alterado se $T$ , $p$ ou as composições dos participantes forem alteradas.

Efeito da Adição/Remoção de um Participante

Adicionar um participante implica em uma perturbação porque sua concentração aumenta bruscamente em um curto espaço de tempo. Isso afeta diretamente o quociente reacional. Para a reação representada por $A(g) \to B(g)$ , por exemplo, a expressão abaixo nos dá o quociente reacional $Q_p$ .

$\begin{align*}Q_p = \f{p_B}{p_A}\end{align*}$

Vamos começar com um sistema em equilíbrio, ou seja, quando $p_B = p_B^{eq}$ e $p_A = p_A^{eq}$ , fazendo, assim, $Q_p = K_p$ . Imagine que adicionemos $A$ ao sistema. Instantaneamente $Q_p < K_p$ e, de acordo com a equação 1, $\Delta G < 0$ , indicando que a reação precisa avançar favorecendo produtos, até que $Q_p$ volte a ser igual a $K_p$ e $\Delta _r G$ volte a ser zero. Assim, a adição de reagentes favorece a formação de produtos.

Se, por outro lado, adicionarmos $B$ , $Q_p > K_p$ e, pela equação 1, $\Delta _r G > 0$ , de modo que a reação precisa retroceder, ou seja, favorecer reagentes até que $Q_p$ e $K_p$ voltem a se igualar, tornando $\Delta _r G = 0$ . Assim, a adição de produtos favorece reagentes. Mas cuidado, existem algumas exceções a esta tendência e, apesar de ser uma aproximação, é importante ter em mente que não há como padronizar tudo na natureza. Essas exceções ocorrem quando mudanças muito pequenas de concentração são feitas em reações mais complexas do que as apresentadas aqui.

Efeito da Pressão

Podemos aumentar a pressão de um sistema reacional de duas formas: por diminuição de volume e por adição de gás inerte. No entanto, o equilíbrio só afetado quando variação é feita por mudança de volume total. A constante de equilíbrio só depende da temperatura. Dessa forma, ao mudarmos a pressão, a composição do sistema muda para obedecer a constante de equilíbrio. Imaginemos a reação representada por:

$\begin{align*}aA(g) \eqseta bB(g)\end{align*}$

A constante de equilíbrio é:

$\begin{align*}K_p = \f{p_B^b}{p_A^a}\end{align*}$

Se diminuirmos o volume total, $p_A$ e $p_B$ aumentam. Se $b > a$ , $p_B^b$ cresce mais rápido que $p_A^a$ e a razão $\f{p_B^b}{p_A^a}$ seria muito maior do que $K_p$ . Para evitar isso, o equilíbrio é deslocado para favorecer a formação de reagentes até $\f{p_B^b}{p_A^a}$ voltar a ser igual à $K_p$ . Perceba que, se $a > b$ , o oposto ocorreria. Se $a > b$ , $p_A^a$ cresce mais rápido que $p_B^b$ e a razão $\f{p_B^b}{p_A^a}$ seria muito menor do que $K_p$ . Para evitar isso, o equilíbrio é deslocado para favorecer a formação de produtos até $\f{p_B^b}{p_A^a}$ voltar a ser igual à $K_p$ . Na prática, aumentar a pressão de um sistema reacional por diminuição de volume favorece o sentido de formação do componente gasoso com menor proporção estequiométrica.

Se, por outro lado, diminuírmos a pressão, por aumento de volume total, o efeito é o oposto. Diminuir a pressão de um sistema reacional por expansão favorece o sentido de formação do componente gasoso com maior proporção estequiométrica. Por exemplo, se $b > a$ , a expansão faz $p_A$ e $p_B$ diminuírem, mas $p_B^b$ diminui mais rápido que $p_A^a$ e a razão $\f{p_B^b}{p_A^a}$ seria muito menor do que $K_p$ . Para evitar isso, o equilíbrio favorece a formação de produtos. Se, por outro lado, $a > b$ , a expansão faz $p_A^a$ diminuir mais rápido que $p_B^b$ e a razão $\f{p_B^b}{p_A^a}$ seria muito maior do que $K_p$ . Para evitar isso, o equilíbrio favorece a formação de reagentes.

A adição de um gás inerte em um reator com $V$ e $T$ constante aumenta a pressão total, porque $p = nRT/V$ e o número de partículas foi aumentado. No entanto, as pressões parciais dos gases participantes da reação ficam inalteradas, pois só dependem de $n_i$ , $V$ e $T$ : $p_i = n_iRT/V$ . Dessa forma, um sistema com pressões parciais de equilíbrio $p_i^{eq}$ para cada participante continuará no mesmo equilíbrio quando um gás inerte for adicionado. Do ponto de vista molecular, não há como os gases participantes da reação perceberem que um gás inerte foi adicionado, pois as interações intermoleculares são ausentes em equilíbrio de gases ideais.

Efeito da Temperatura

Como a constante de equilíbrio só depende da temperatura, de todos os efeitos vistos aqui, este é o único que, efetivamente, muda a constante de equilíbrio. Se o aquecimento aumentar a constante de equilíbrio, este estará mais deslocado aos produtos do que antes do aquecimento. Se o aquecimento diminuir a constante de equilíbrio, este estará mais deslocado aos reagentes do que antes do aquecimento.

Mas como saber se o aquecimento aumenta ou diminui a constante de equilíbrio? Sabemos que $K_p^\circ$ está relacionada com $\Delta_r G^\circ$ por:

$\begin{align*}\ln{K_p^\circ} = -\f{\Delta_r G^\circ}{RT}\end{align*}$

Como temos interesse na mudança de temperatura, derivaremos ambos os lados dessa equação em relação à $T$ :

$\begin{align*}&\dv{\ln{K_p^\circ}}{T} = -\f{1}{R}\dv{(\Delta_r G^\circ/T)}{T}\\&\dv{\ln{K_p^\circ}}{T} = -\f{1}{R}\f{\dv{(\Delta_r G^\circ)}{T}T - \Delta_r G^\circ}{T^2}\\&\dv{\ln{K_p^\circ}}{T} = -\f{1}{R}\f{-\Delta_r S^\circ T - \Delta_r G^\circ}{T^2}\\&\dv{\ln{K_p^\circ}}{T} = -\f{1}{R}\f{-\Delta_r S^\circ T - \Delta_r H^\circ + T\Delta_r S^\circ}{T^2}\\&\dv{\ln{K_p^\circ}}{T} = -\f{1}{R}\f{-\Delta_r H^\circ}{T^2}\\&\boxed{\dv{\ln{K_p^\circ}}{T} = \f{\Delta_r H^\circ}{RT^2}}\end{align*}$

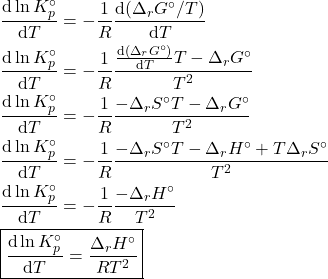
Essa equação é conhecida como equação de van’t Hoff. Repare que o sinal da derivada é o mesmo do $\Delta_r H^\circ$ . Para reações endentálpicas ( $\Delta_r H^\circ > 0$ ), a constante de equilíbrio aumenta com $T$ e, após o aquecimento, o sistema estará mais deslocado para os produtos do que antes. Para esse mesmo tipo de reação, se diminuírmos $T$ , a constante de equilíbrio também diminuirá e o estado resfriado está mais deslocado para os reagentes do que o original.

Para reações exentálpicas ( $\Delta_r H^\circ < 0$ ), por outro lado, a constante de equilíbrio diminui com a temperatura. Assim, ao aquecer esse sistema, produzimos um estado com menor constante de equilíbrio e, logo, mais deslocado para os reagentes do que o original. Por outro lado, para esse mesmo tipo de reação, se resfriamos o sistema, aumentamos a constante de equilíbrio, de modo que o sistema resfriado está mais deslocado para os produtos do que o original.

Para calcular a constante de equilíbrio de outras temperaturas, podemos simplesmente integrar a equação de van’t Hoff.

$\begin{align*}&\dv{\ln{K_p^\circ}}{T} = \f{\Delta_r H^\circ}{RT^2}\\&\dd{\ln{K_p^\circ}} = \f{\Delta_r H^\circ}{RT^2}\dd{T}\\&\int_{\ln{K_p^\circ (T_1)}}^{\ln{K_p^\circ (T_2)}}\dd{\ln{K_p^\circ}} = \int_{}^{}\f{\Delta_r H^\circ}{RT^2}\dd{T}\\&\ln{K_p^\circ (T_2)} - \ln{K_p^\circ (T_1)} = \f{1}{R}\int_{T_1}^{T_2}\f{\Delta_r H^\circ}{T^2}\dd{T}\end{align*}$

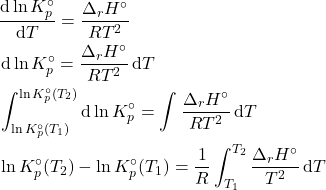
E agora fazemos uma aproximação, dizendo que $\Delta_r H^\circ$ independe de $T$ no intervalo de temperaturas considerado.

$\begin{align*}&\ln{K_p^\circ (T_2)} - \ln{K_p^\circ (T_1)} = \f{\Delta_r H^\circ}{R}\int_{T_1}^{T_2}\f{1}{T^2}\dd{T}\\&\ln{K_p^\circ (T_2)} - \ln{K_p^\circ (T_1)} = \f{\Delta_r H^\circ}{R}\colchetes{-\f{1}{T_2} - \parentesis{-\f{1}{T_1}}}\\&\boxed{\ln{K_p^\circ (T_2)} = \ln{K_p^\circ (T_1)} + \f{\Delta_r H^\circ}{R}\colchetes{\f{1}{T_1} - \f{1}{T_2}}}\end{align*}$

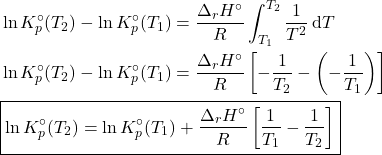
Exercícios

1) Em $\mathrm{1105~K}$ , o valor de $K_p^\circ$ para a reação equacionada por $\mathrm{SO_2(g) + \f{1}{2}O_2(g) \rightleftharpoons SO_3(g)}$ é $0.63$ . Calcule:
a) A energia livre de Gibbs padrão de reação, a $\mathrm{1105~K}$ .
b) A energia livre de reação quando as pressões parciais de $\mathrm{SO_2}$ , $\mathrm{O_2}$ e $\mathrm{SO_3}$ são, respectivamente, $\mathrm{1~bar}$ , $\mathrm{25~bar}$ e $\mathrm{2~bar}$ , respectivamente. Interprete o resultado.

Gabarito

a) $\mathrm{4.24~kJ~mol^{-1}}$ .

b) $-\mathrm{4.17~kJ~mol^{-1}}$ . O valor negativo indica que o sistema ainda não atingiu o equilíbrio e a reação precisa avançar ( $\xi > 0$ ) até que $G$ atinja o seu valor mínimo e $\Delta _r G$ seja nulo.

Resolução

2) A reação equacionada por: $\mathrm{N_2O_3(g) \rightleftharpoons NO_2(g) + NO(g)}$ foi estudada a $\mathrm{25~\celsius}$ com uma quantidade inicial de trióxido igual a $\mathrm{1~mol}$ . A reação avança $\mathrm{0.3~mol}$ até atingir o equilíbrio em uma pressão total de $\mathrm{1~bar}$ . Calcule $K_p^\circ$ e $\Delta_r G^\circ$ para a reação.

Gabarito

a) $K_p^\circ = \mathrm{0.099}$ e $\Delta _r G^\circ = \mathrm{5.76~kJ~mol^{-1}}$ .

Resolução

3) A reação equacionada por: $\mathrm{NH_4HS(s) \rightleftharpoons NH_3(g) + H_2S(g)}$ foi estudada a $\mathrm{25~\celsius}$ . A pressão total medida no equilíbrio foi de $\mathrm{0.67~bar}$ . Calcule a constante de equilíbrio padrão em função das pressões parciais e a energia livre de Gibbs padrão de reação.

Gabarito

a) $K_p^\circ = \mathrm{0.112}$ e $\Delta _r G^\circ = \mathrm{5.4~kJ~mol^{-1}}$ .

Resolução

4) Para a reação equacionada por $\mathrm{CH_4(g) + 2H_2S(g) \rightleftharpoons CS_2(g) + 4H_2(g)}$ , $K_p^\circ = \mathrm{2.05\times 10^9}$ a $\mathrm{25~\celsius}$ . Calcule $K_p^\circ$ e $K_c^\circ$ nessa mesma temperatura para a reação representada por $\mathrm{\f{1}{2}CS_2(g) + 2H_2(g) \rightleftharpoons \f{1}{2}CH_4(g) + H_2S(g)}$ .

Gabarito

a) $K_p^\circ = \mathrm{2.2\times 10^{-5}}$ e $K_c^\circ = \mathrm{5.4\times 10^{-4}}$ .

Resolução

5) Considere a reação equacionada por:

$\begin{align*}\mathrm{\f{1}{2}I_2(g) + \f{1}{2}Br_2(g) \rightleftharpoons IBr (g)}\end{align*}$

A dependência da constante de equilíbrio dessa reação com a temperatura é dada pela equação empírica:

$\begin{align*}\log{K_p^\circ} = \f{\mathrm{277.4~K}}{T} + 0.3811\end{align*}$

Calcule a energia de Gibbs padrão, a entalpia padrão e a entropia padrão de reação a $\mathrm{25~\celsius}$ .

Gabarito

$\Delta _r G^\circ = \mathrm{-7.5~kJ~mol^{-1}}$ , $\Delta _r H^\circ = \mathrm{-5.3~kJ~mol^{-1}}$ e $\Delta _r S^\circ = \mathrm{7.3~J~K^{-1}~mol^{-1}}$ .

Resolução

6) $\mathrm{2~mol}$ de $\mathrm{PCl_5(g)}$ são aquecidos até $\mathrm{502~K}$ até que o equilíbrio seja atingido a uma pressão total de $\mathrm{1~atm}$ . Calcule a composição no equilíbrio e também a porcentagem de reagente decomposta em tricloreto e gás cloro, sabendo que $K_p^\circ = 0.4461$ .

Gabarito

$\mathrm{0.9~mol~PCl_5}$ , $\mathrm{1.1~mol~PCl_3}$ e $\mathrm{1.1~mol~Cl_2}$ . $55\%$ do reagente sofreu decomposição.

Resolução

7) Dadas as seguintes energias de Gibbs padrão de formação, a $\mathrm{25~\celsius}$ :

	$\mathrm{CO(g)}$	$\mathrm{CO_2(g)}$	$\mathrm{H_2O(g)}$	$\mathrm{H_2O(l)}$
$\Delta_f G^\circ~\mathrm{(kJ~mol^{-1})}$	$\mathrm{-137.17}$	$\mathrm{-394.36}$	$\mathrm{-228.57}$	$\mathrm{-237.13}$

a) Encontre a energia de Gibbs padrão de reação e a constante de equilíbrio padrão em função das pressões parciais para a reação equacionada por: $\mathrm{CO(g) + H_2O(g) \rightleftharpoons CO_2(g) + H_2(g)}$ .
b) Calcule a pressão de vapor da água pura a $\mathrm{298~K}$ .