Equilíbrio Líquido Líquido (ELL)
A Abordagem Termodinâmica
(1) ![]()
Que é um valor sempre negativo, independente das frações molares.
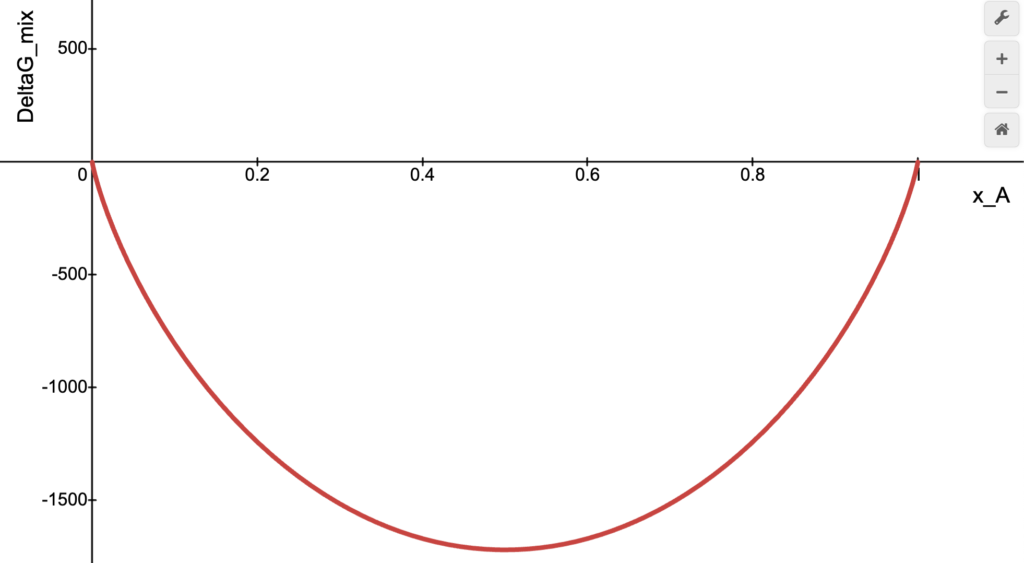
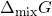 para líquidos que formam soluções
para líquidos que formam soluções 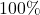 ideais. Construído no desmos.
ideais. Construído no desmos.Mas não há a necessidade de dois líquidos serem tão semelhantes para serem completamente miscíveis. Etanol (![]() ) e água (
) e água (![]() ), por exemplo, formam soluções com consideráveis desvios da idealidade e, ainda assim, são completamente miscíveis. Se descrevermos o desvio da idealidade usando a equação de Margules de um parâmetro (
), por exemplo, formam soluções com consideráveis desvios da idealidade e, ainda assim, são completamente miscíveis. Se descrevermos o desvio da idealidade usando a equação de Margules de um parâmetro (![]() ), sabemos que a energia livre de Gibbs de mistura é dada pela equação 2.
), sabemos que a energia livre de Gibbs de mistura é dada pela equação 2.
(2) ![]()
Repare no último termo do parêntesis: ![]() . Se as interações
. Se as interações ![]() forem favoráveis,
forem favoráveis, ![]() é bem negativo, o que faria
é bem negativo, o que faria ![]() negativo e tornaria
negativo e tornaria ![]() ainda mais negativo do que o previsto para uma solução ideal (os líquidos ainda seriam completamente miscíveis).
ainda mais negativo do que o previsto para uma solução ideal (os líquidos ainda seriam completamente miscíveis).
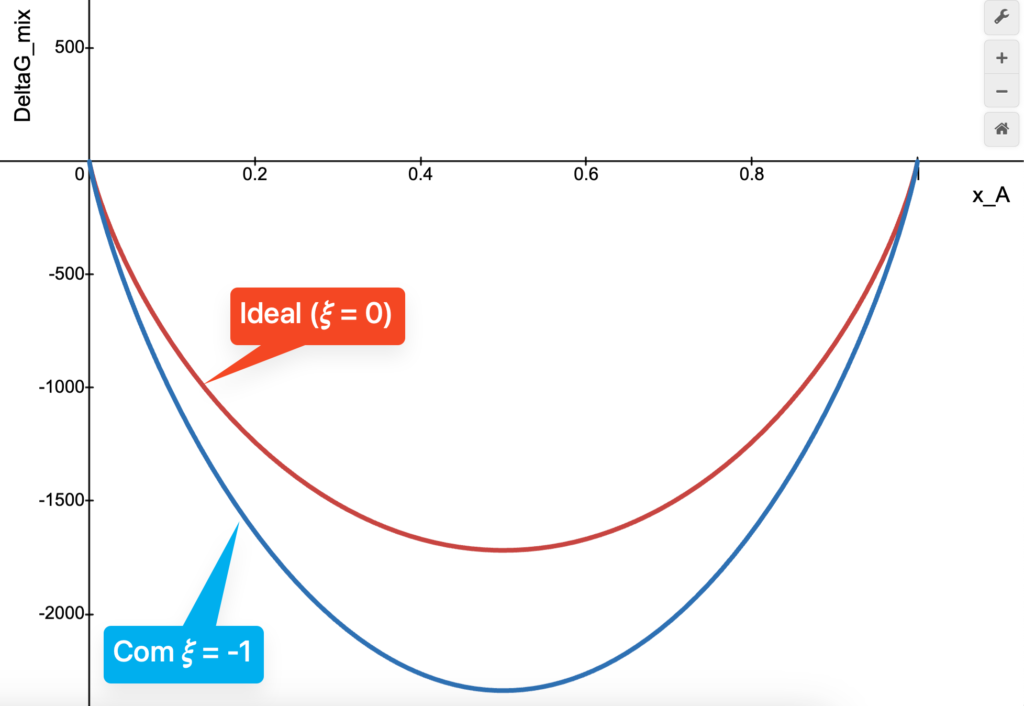
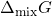 ainda mais negativo para uma solução com
ainda mais negativo para uma solução com 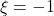 . Construído no desmos.
. Construído no desmos.Vamos imaginar a situação oposta agora. Se ![]() for suficientemente positivo (interações
for suficientemente positivo (interações ![]() desfavoráveis),
desfavoráveis), ![]() pode ser tão positivo que supere o termo
pode ser tão positivo que supere o termo ![]() , fazendo
, fazendo ![]() tornar-se positivo em algumas composições (e ainda sobrevive negativo em outras). Como a miscibilidade ocorre apenas em uma faixa de composições, estamos diante de um caso de miscibilidade parcial.
tornar-se positivo em algumas composições (e ainda sobrevive negativo em outras). Como a miscibilidade ocorre apenas em uma faixa de composições, estamos diante de um caso de miscibilidade parcial.
O gráfico de ![]() para uma solução com
para uma solução com ![]() , por exemplo, está mostrado abaixo. Perceba que, apesar das interações serem desfavoráveis, ainda existem faixas de composições onde
, por exemplo, está mostrado abaixo. Perceba que, apesar das interações serem desfavoráveis, ainda existem faixas de composições onde ![]() é negativo. Essas faixas são:
é negativo. Essas faixas são:
1. ![]() : que são as soluções ricas em
: que são as soluções ricas em ![]() . A pouca quantidade de
. A pouca quantidade de ![]() é insuficiente para tornar
é insuficiente para tornar ![]() positivo.
positivo.
2. ![]() : que são as soluções ricas em
: que são as soluções ricas em ![]() . A pouca quantidade de
. A pouca quantidade de ![]() é insuficiente para tornar
é insuficiente para tornar ![]() positivo.
positivo.
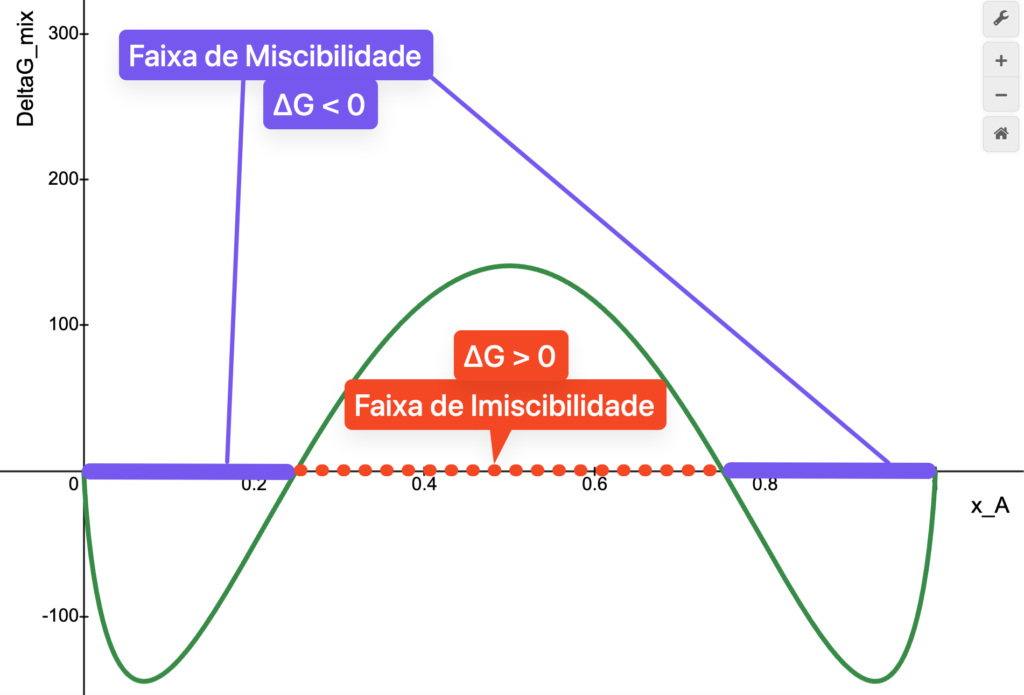
 à temperatura ambiente. A faixa de miscibilidade é
à temperatura ambiente. A faixa de miscibilidade é 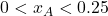 e
e 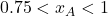 . Construído no desmos.
. Construído no desmos.A faixa de composições onde existem consideráveis quantidades relativas de ![]() e
e ![]() sofrem a penalidade de ter seu
sofrem a penalidade de ter seu ![]() positivo por conta das interações desfavoráveis. Lembre-se que
positivo por conta das interações desfavoráveis. Lembre-se que ![]() é o descritor da espontaneidade e equilíbrio em
é o descritor da espontaneidade e equilíbrio em ![]() e
e ![]() constantes, que são as condições que usamos em laboratório para misturar líquidos. Dessa forma, no exemplo apresentado, a solução com composição
constantes, que são as condições que usamos em laboratório para misturar líquidos. Dessa forma, no exemplo apresentado, a solução com composição ![]() e
e ![]() não se forma. No lugar dela, a natureza se encarrega de minimizar
não se forma. No lugar dela, a natureza se encarrega de minimizar ![]() , separando a matéria em duas soluções conjugadas, duas fases líquidas que apresentam as composições dos dois mínimos do gráfico anterior.
, separando a matéria em duas soluções conjugadas, duas fases líquidas que apresentam as composições dos dois mínimos do gráfico anterior.
1. Fase 1: solução com ![]() e
e ![]() , que é uma solução rica em
, que é uma solução rica em ![]() e o pouco de
e o pouco de ![]() dissolvido é chamado de solubilidade.
dissolvido é chamado de solubilidade.
2. Fase 2: solução com ![]() e
e ![]() , que é uma solução rica em
, que é uma solução rica em ![]() e o pouco de
e o pouco de ![]() dissolvido é, também, sua solubilidade.
dissolvido é, também, sua solubilidade.
A temperatura afeta a miscibilidade de líquidos. Líquidos que são parcialmente miscíveis em ![]() podem se tornar miscíveis em temperaturas mais altas. A razão disso que é o aquecimento aumenta a energia cinética média das moléculas de
podem se tornar miscíveis em temperaturas mais altas. A razão disso que é o aquecimento aumenta a energia cinética média das moléculas de ![]() e
e ![]() , enfraquecendo as interações
, enfraquecendo as interações ![]() desfavoráveis e fazendo
desfavoráveis e fazendo ![]() diminuir. A temperatura na qual o valor de
diminuir. A temperatura na qual o valor de ![]() diminui o suficiente para que o gráfico de
diminui o suficiente para que o gráfico de ![]() apresente valores negativos em qualquer composição é chamada de temperatura consoluta superior ou temperatura crítica (
apresente valores negativos em qualquer composição é chamada de temperatura consoluta superior ou temperatura crítica (![]() ). O gráfico abaixo mostra as curvas de
). O gráfico abaixo mostra as curvas de ![]() para diferentes valores de
para diferentes valores de ![]() , alterados pela mudança de temperatura.
, alterados pela mudança de temperatura.

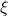 e, em
e, em 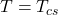 , todos os valores de
, todos os valores de 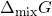 tornam-se negativos em quaquer composição. Construído no desmos.
tornam-se negativos em quaquer composição. Construído no desmos.Esse gráfico mostra, ainda, outro ponto interessante: os dois mínimos das curvas com ![]() ,
, ![]() ,
, ![]() e
e ![]() variam para maiores valores de concentração de soluto. Isso indica um aumento de solubilidade causado pelo aquecimento. Se colocarmos essas solubilidades no eixo horizontal e a temperatura no eixo vertical obteremos um diagrama de fases de líquidos parcialmente miscíveis.
variam para maiores valores de concentração de soluto. Isso indica um aumento de solubilidade causado pelo aquecimento. Se colocarmos essas solubilidades no eixo horizontal e a temperatura no eixo vertical obteremos um diagrama de fases de líquidos parcialmente miscíveis.
Os Diagramas de Fases
Para Líquidos com Temperatura Consoluta Superior
Líquidos que apresentam temperatura consoluta superior possuem um diagrama de fases com a aparência do mostrado na figura abaixo (ele foi tirado da excelente plataforma em simulações de Físico-Química: LearnChemE).
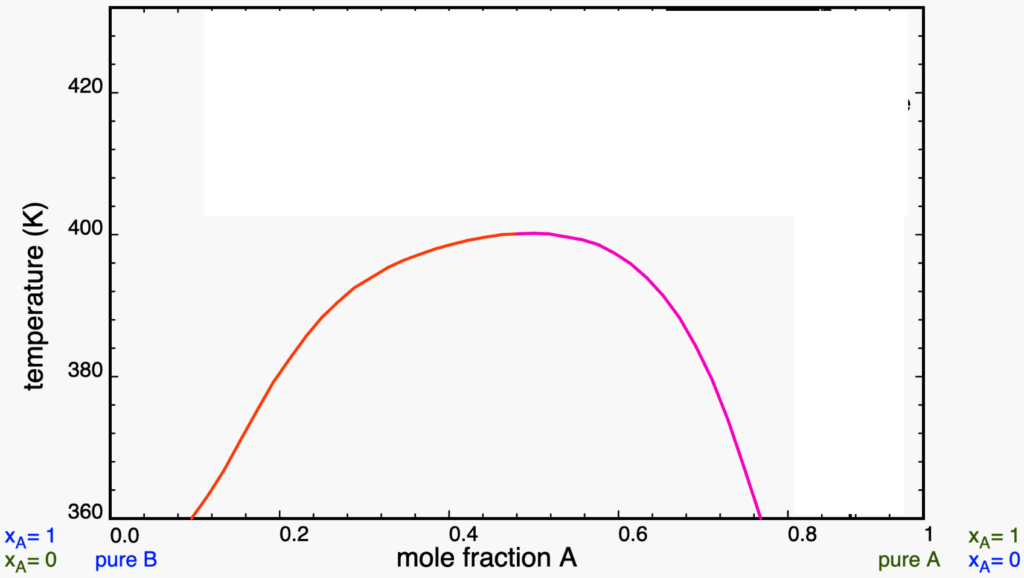
Comecemos a discutir o diagrama na chamada adição isotérmica, ou seja, partindo de ![]() puro (
puro (![]() ), adicionamos, gradativa e isotermicamente,
), adicionamos, gradativa e isotermicamente, ![]() para mudar a composição global do sistema, representada no eixo horizontal do diagrama. Então começamos com o ponto mostrado abaixo, na temperatura de
para mudar a composição global do sistema, representada no eixo horizontal do diagrama. Então começamos com o ponto mostrado abaixo, na temperatura de ![]() e, obviamente,
e, obviamente, ![]() .
.
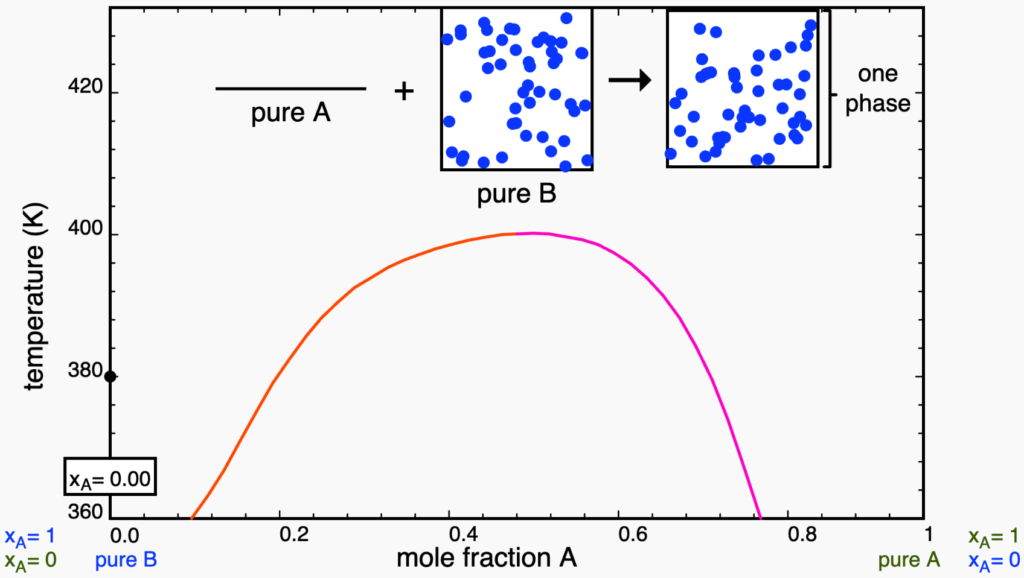
 puro. Retirado da plataforma LearnChemE.
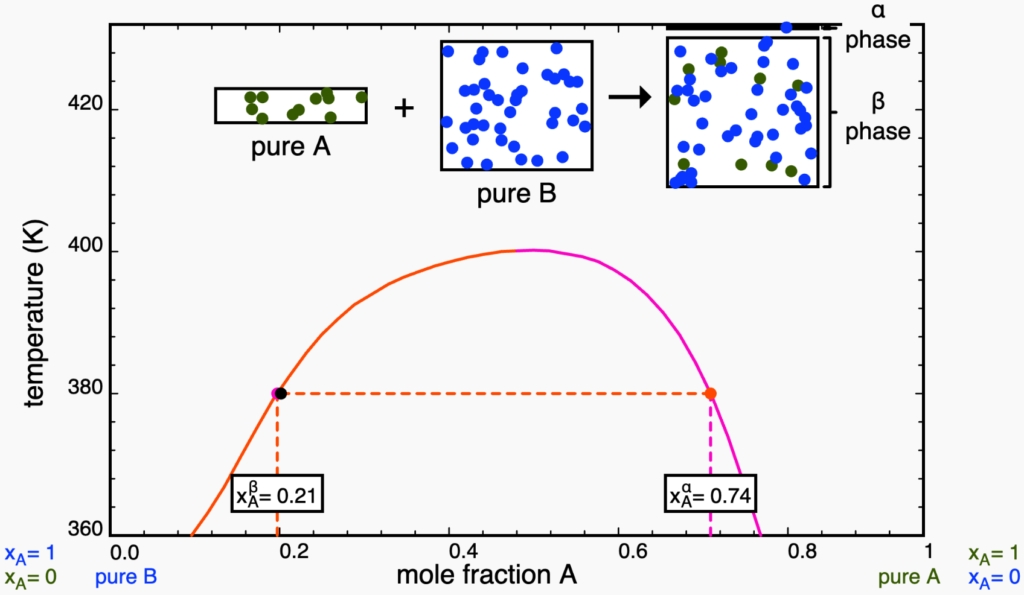
puro. Retirado da plataforma LearnChemE.Ao adicionar ![]() , a composição global muda até que o ponto toque a linha binal em vermelho, entrando na região bifásica. Como qualquer ponto em região bifásica, as composições das fases são dadas pelas extremidades da linha de amarração, como mosttrado na figura abaixo. Perceba que a linha de amarração precisa, obrigatoriamente, conectar um ponto de cada curva binodal (em vermelho e rosa). É importante notar, ainda, que a quantidade da nova fase (chamada de
, a composição global muda até que o ponto toque a linha binal em vermelho, entrando na região bifásica. Como qualquer ponto em região bifásica, as composições das fases são dadas pelas extremidades da linha de amarração, como mosttrado na figura abaixo. Perceba que a linha de amarração precisa, obrigatoriamente, conectar um ponto de cada curva binodal (em vermelho e rosa). É importante notar, ainda, que a quantidade da nova fase (chamada de ![]() ) é muito pequena, coerente com a regra da alavanca, pois o ponto está muito longe da binodal rosa. Assim, nesse ponto, quase todas as partículas do sistema ainda estão na fase
) é muito pequena, coerente com a regra da alavanca, pois o ponto está muito longe da binodal rosa. Assim, nesse ponto, quase todas as partículas do sistema ainda estão na fase ![]() , rica em
, rica em ![]() .
.
A continuação da adição de ![]() nos leva até o ponto representado abaixo. Perceba que a linha de amarração é exatamente a mesma da última figura, ou seja, as composições das fases
nos leva até o ponto representado abaixo. Perceba que a linha de amarração é exatamente a mesma da última figura, ou seja, as composições das fases ![]() e
e ![]() não se alteram com a adição de
não se alteram com a adição de ![]() . Não se perturbe com isso, achando que ambas fases deveriam enriquecer em
. Não se perturbe com isso, achando que ambas fases deveriam enriquecer em ![]() . Perceba, na figura, que as moléculas de
. Perceba, na figura, que as moléculas de ![]() e
e ![]() se redistribuem de forma totalmente diferente do último ponto descrito para garantir que as composições fiquem fixas em
se redistribuem de forma totalmente diferente do último ponto descrito para garantir que as composições fiquem fixas em ![]() e
e ![]() , fazendo com que a energia de Gibbs seja mínima em cada fase.
, fazendo com que a energia de Gibbs seja mínima em cada fase.
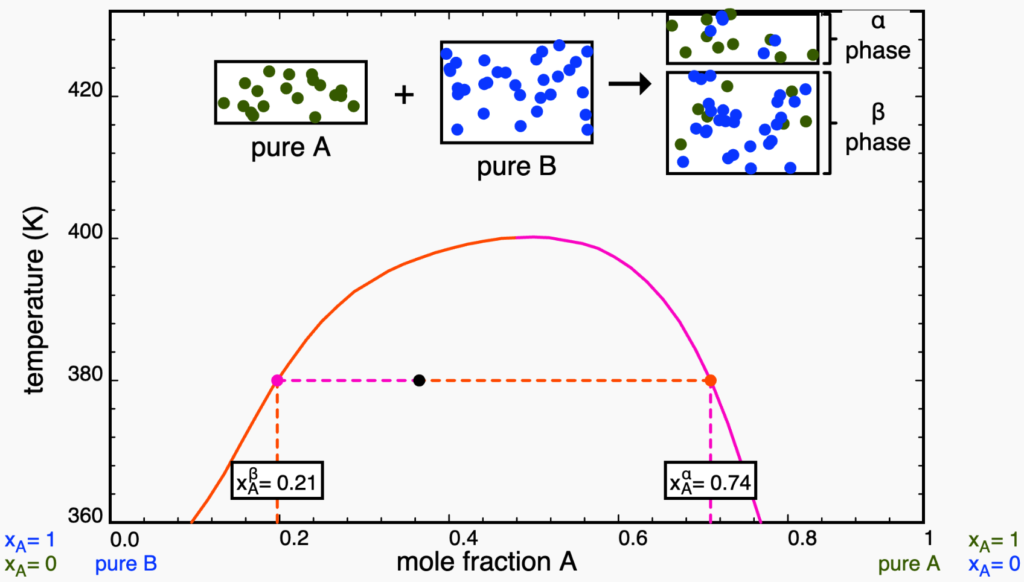
Se adicionarmos ![]() até atingirmos o ponto na curva em rosa, a regra da alavanca nos garante que quase todas as partículas do sistema estarão na fase
até atingirmos o ponto na curva em rosa, a regra da alavanca nos garante que quase todas as partículas do sistema estarão na fase ![]() , com apenas uma gotícula de
, com apenas uma gotícula de ![]() .
.
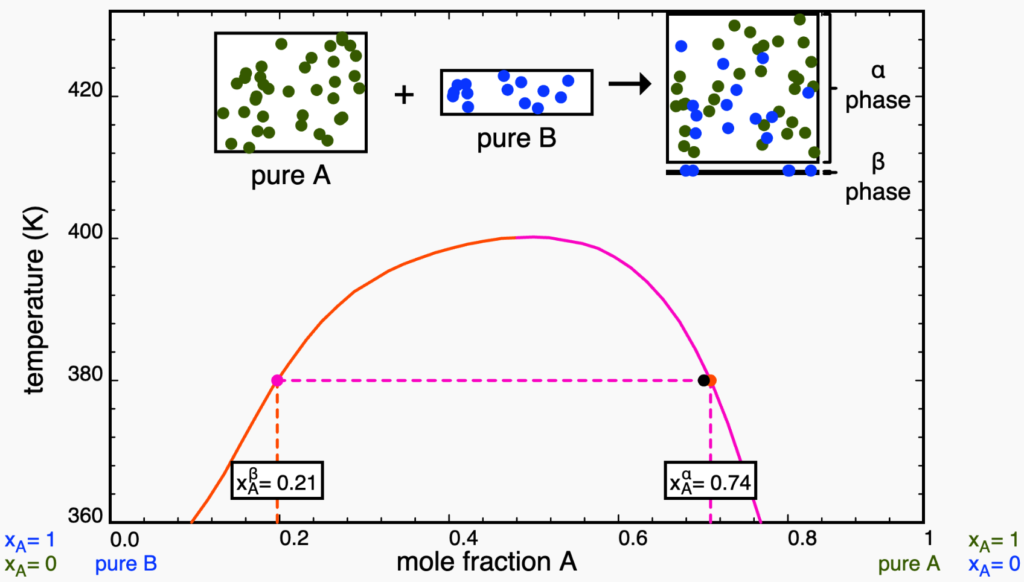
A partir desse ponto, qualquer adição de ![]() irá homogeneizar o sistema e todo o
irá homogeneizar o sistema e todo o ![]() dissolverá todo o
dissolverá todo o ![]() , pois voltamos à faixa de miscibilidade dos líquidos.
, pois voltamos à faixa de miscibilidade dos líquidos.

Se quisermos fazer o ponto tocar o eixo ![]() à direita (com
à direita (com ![]() ) seria necessário adicionar uma quantidade infinita de
) seria necessário adicionar uma quantidade infinita de ![]() , pois sempre existirão traços de
, pois sempre existirão traços de ![]() no sistema (uma vez que começamos com
no sistema (uma vez que começamos com ![]() puro).
puro).
Considere agora o aquecimento de um sistema heterogêneo de composição dada pelo ponto abaixo.
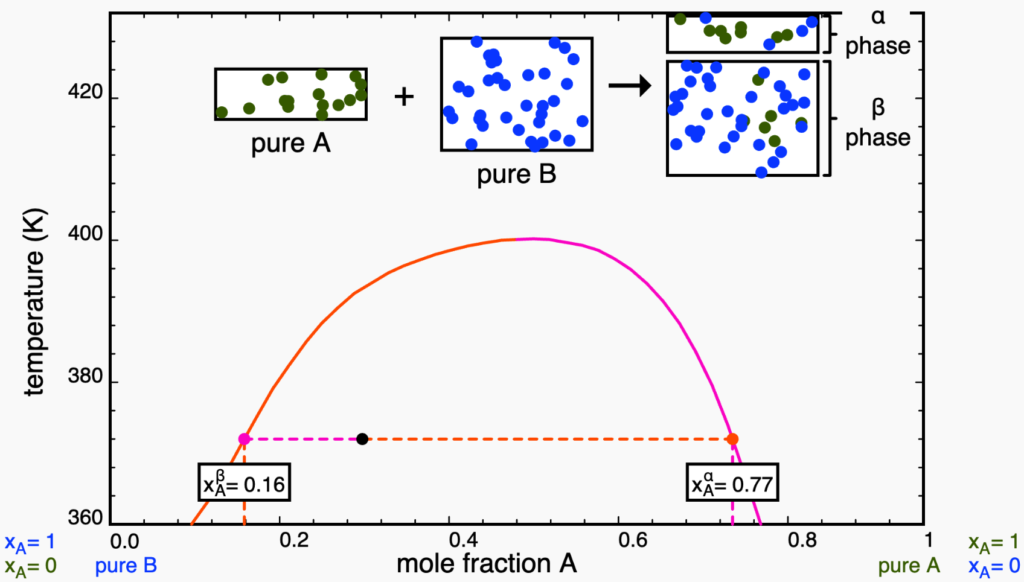
O aumento da temperatura diminui o desvio da idealidade, enfraquecendo as interações desfavoráveis e aumentando a solubilidade (como discutimos na seção sobre Termodinâmica). Dessa forma, o ponto se desloca verticalmente para cima, na isopleta, e as extremidades da linha de amarração se aproximam uma da outra, indicando o aumento da solubilidade.
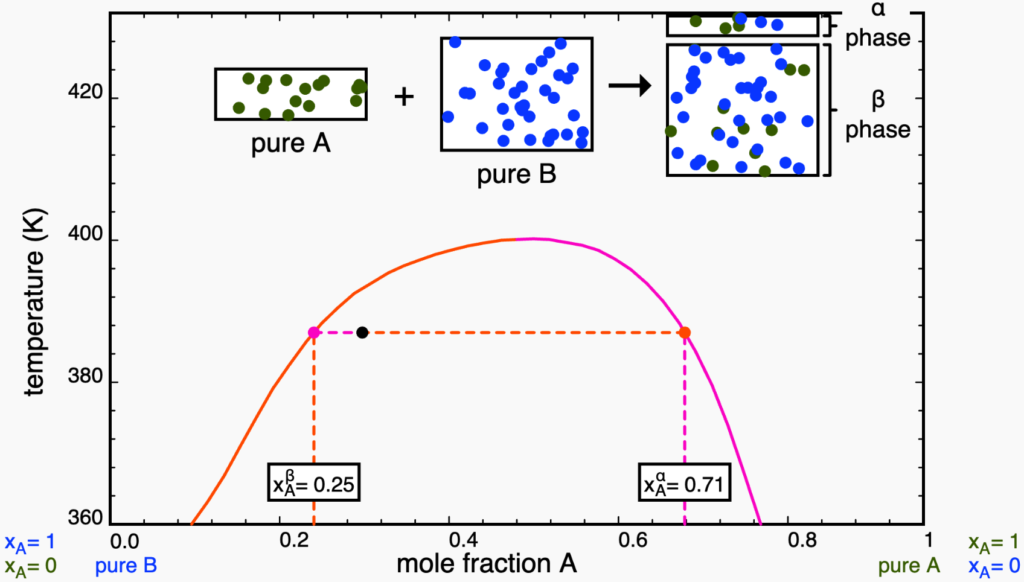
Se continuarmos a aquecer o sistema até atingir a fronteira com a região monofásica, teremos uma última gota de uma das fases e a outra fase apresenta a composição global.
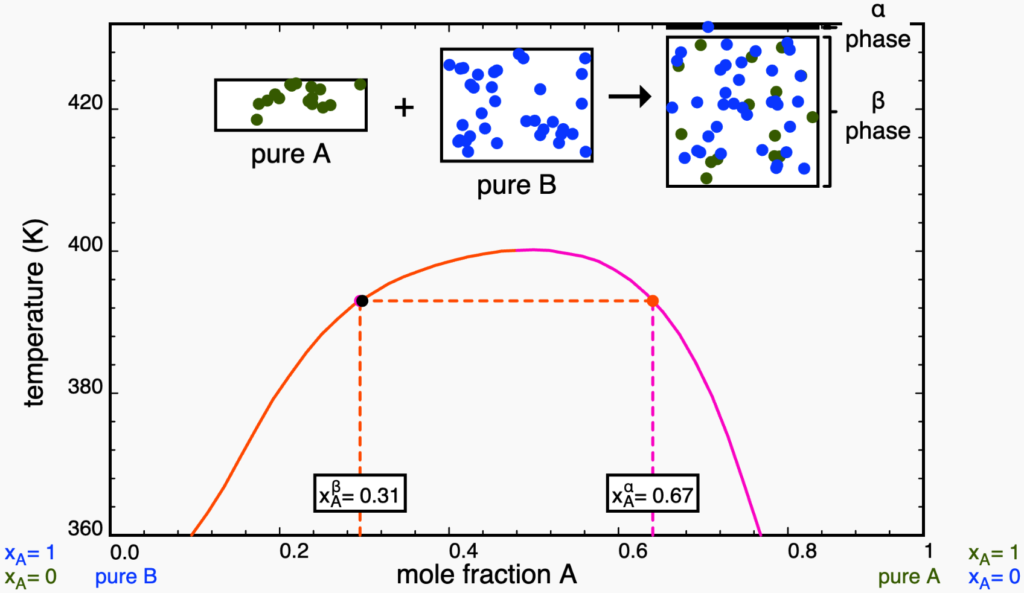
A partir deste ponto, qualquer aquecimento irá homogeneizar o sistema, formando uma solução com a composição da isopleta.
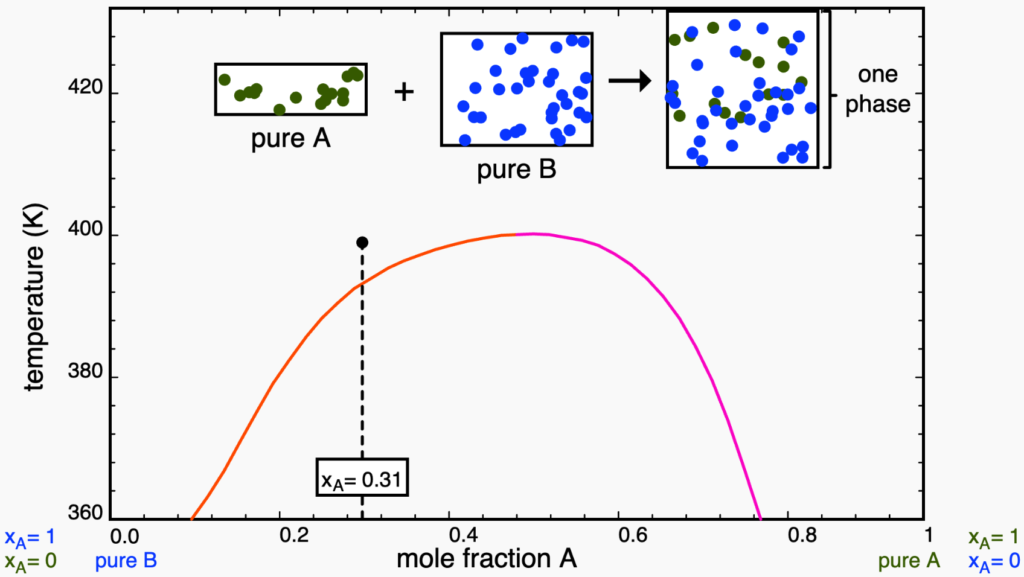
Para Líquidos com Temperatura Consoluta Inferior
Em algumas situações (como o sistema “água-trietilamina”), a situação oposta à descrita na subseção anterior ocorre. A água e a trietilamina são capazes de realizar ligações de hidrogênio, como mostrado abaixo:
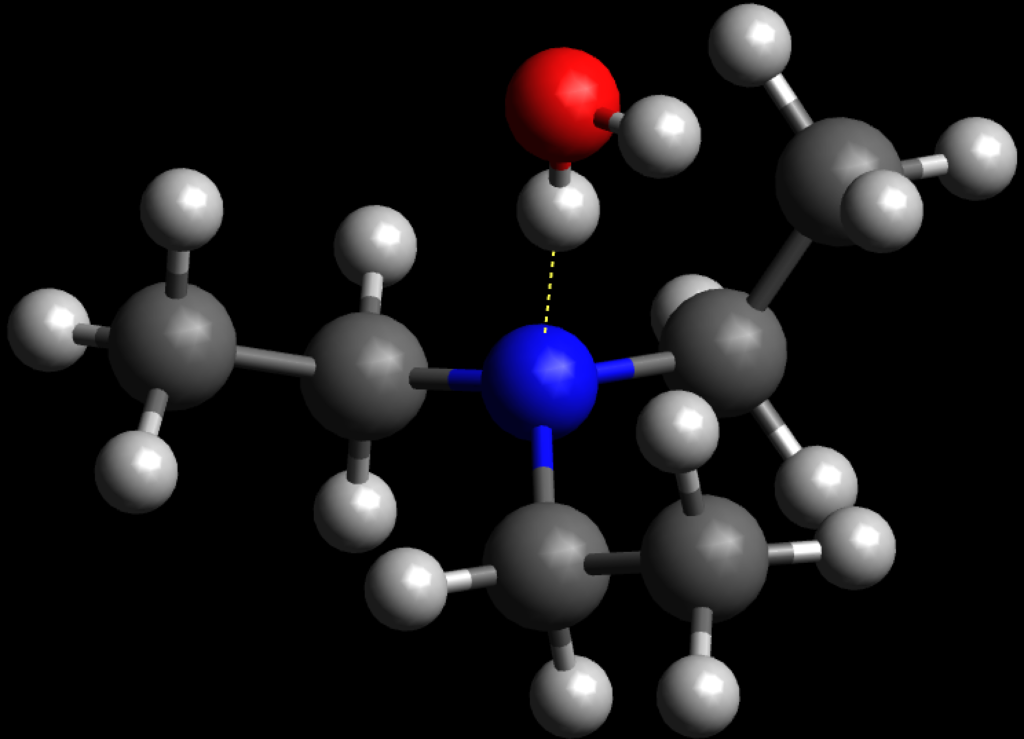
Essas interações específicas (que só ocorrem em alguns pares de substâncias) não são muito favoráveis quando a mistura é aquecida. Assim, se diminuirmos a temperatura desse tipo de sistema, as substâncias são (em contraste com o último caso) solúveis e, ao aumentar a temperatura, ocorre a quebra das ligações de hidrogênio responsáveis pela solubilização e a consequente separação de fases.
Esse comportamento se manifesta no diagrama com um temperatura crítica inferior ou temperatura consoluta inferior (![]() ), como mostrado na figura abaixo.
), como mostrado na figura abaixo.
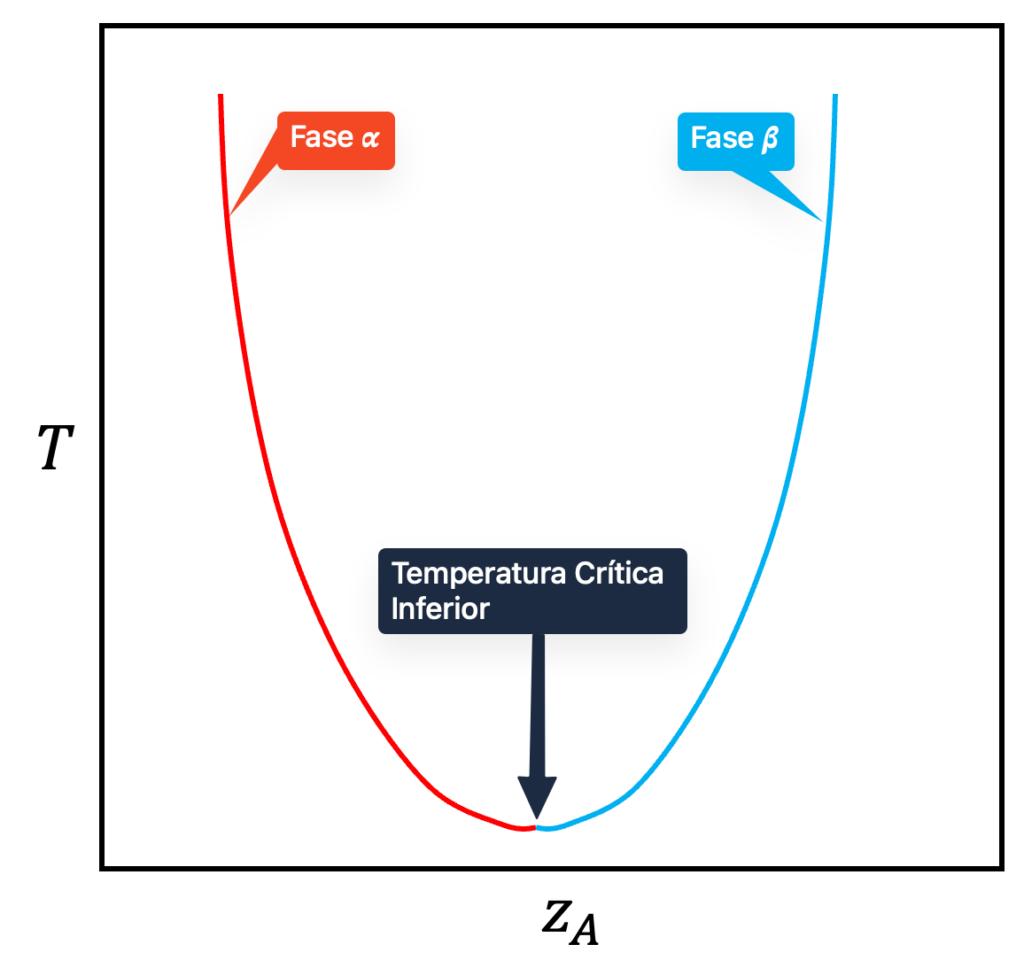
Para Líquidos com Temperaturas Consolutas Superior e Inferior
Alguns líquidos apresentam uma combinação dos dois últimos comportamentos, isto é, solubilizam-se por formarem complexos moleculares em temperaturas baixas (pelas ligações de hidrogênio sobreviventes) e também se solubilizam pela diminuição do desvio da idealidade ao aquecermos. Isso produz duas temperaturas críticas no diagrama do ELL: ![]() e
e ![]() , como mostrado na figura abaixo.
, como mostrado na figura abaixo.
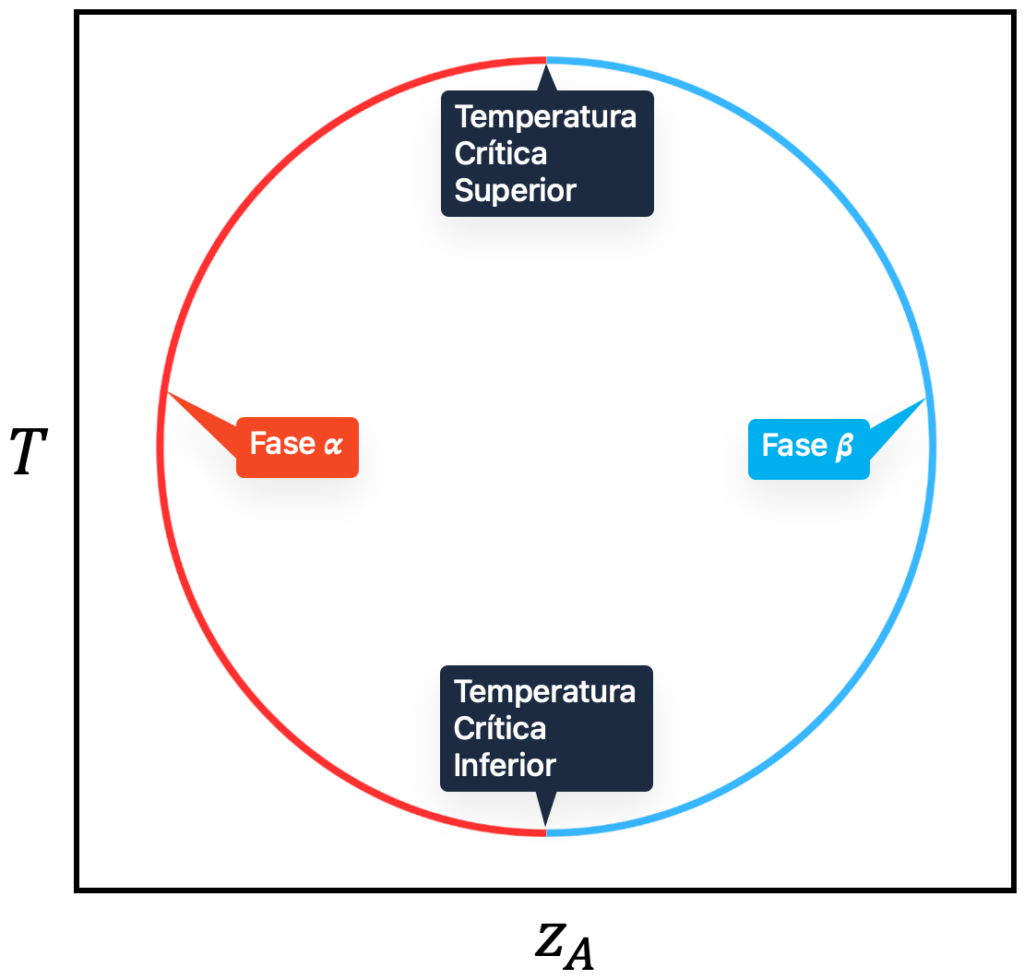
O Coeficiente de Partição
Vamos supor que tenhamos um sistema bifásico (ELL), cujas fases são ![]() e
e ![]() . A fase
. A fase ![]() é rica em
é rica em ![]() e a fase
e a fase ![]() é rica em
é rica em ![]() . Se adicionarmos um soluto
. Se adicionarmos um soluto ![]() ao sistema, as moléculas de
ao sistema, as moléculas de ![]() se distribuirão pelos dois líquidos, em concentrações diferentes, mas respeitando o equilíbrio termodinâmico dado pela equação 3.
se distribuirão pelos dois líquidos, em concentrações diferentes, mas respeitando o equilíbrio termodinâmico dado pela equação 3.
(3) ![]()
Vimos que o potencial químico do soluto em uma solução real é dado pela equação 4.
(4) ![]()
Usando a escala de concentrações molares (![]() ), temos que:
), temos que:
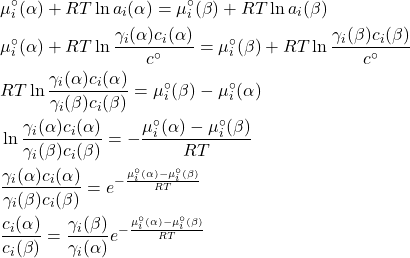
É possível chegar à mesma expressão usando a relação fundamental ![]() . O primeiro membro é a razão entre as solubilidades do soluto
. O primeiro membro é a razão entre as solubilidades do soluto ![]() em cada fase e é chamado de coeficiente de partição ou constante de distribuição do soluto
em cada fase e é chamado de coeficiente de partição ou constante de distribuição do soluto ![]() nas fases
nas fases ![]() e
e ![]() (
(![]() , na equação 5). Perceba que as concentrações que aparecem são referentes às fases e não aos solventes puros, mas, em alguns casos, há tão pouco
, na equação 5). Perceba que as concentrações que aparecem são referentes às fases e não aos solventes puros, mas, em alguns casos, há tão pouco ![]() em
em ![]() e
e ![]() em
em ![]() , que dizemos que a constante de distribuição é aproximadamente a razão entre as solubilidades do soluto
, que dizemos que a constante de distribuição é aproximadamente a razão entre as solubilidades do soluto ![]() nos solventes puros.
nos solventes puros.
(5) 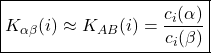
É importante dizer que essa grandeza não é, de fato, fixa a ![]() e
e ![]() constantes.
constantes. ![]() varia quando adicionamos mais
varia quando adicionamos mais ![]() ao sistema, pois isso afeta os coeficientes de atividade e, logo, as concentrações. No entanto, valores tabelados de
ao sistema, pois isso afeta os coeficientes de atividade e, logo, as concentrações. No entanto, valores tabelados de ![]() são apresentados com duas aproximações principais:
são apresentados com duas aproximações principais:
– Desprezando a presença de ![]() e
e ![]() um no outro (como se as fases fossem puras).
um no outro (como se as fases fossem puras).
– Considerando soluções extremamente diluídas (diluídas-ideais), onde os coeficientes de atividades são próximos a ![]() .
.
Um dos mais famosos coeficientes de partição é o coeficiente de partição octanol-água (![]() ), definido pela equação 6.
), definido pela equação 6.
(6) 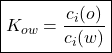
O conhecimento dessa grandeza revela informações sobre a polaridade do soluto. Se ![]() for elevado o soluto apresenta baixa polaridade, uma vez que sua concentração é maior em octan-1-ol. Se
for elevado o soluto apresenta baixa polaridade, uma vez que sua concentração é maior em octan-1-ol. Se ![]() for baixo o soluto apresenta uma polaridade mais alta, uma vez que sua concentração é maior em água. Estudos envolvendo a biodisponibilidade de fármacos no corpo humano usam o coeficiente de partição para prever se eles passarão ou não pela membrana plasmática celular, que é uma bicamada fosfolipídica.
for baixo o soluto apresenta uma polaridade mais alta, uma vez que sua concentração é maior em água. Estudos envolvendo a biodisponibilidade de fármacos no corpo humano usam o coeficiente de partição para prever se eles passarão ou não pela membrana plasmática celular, que é uma bicamada fosfolipídica.
O Equilíbrio Líquido-Líquido-Vapor (ELLV)
Soluções de líquidos parcialmente miscíveis podem apresentar graves desvios da idealidade. Esses desvios, eventualmente, possibilitam a existência de azeótropos no equilíbrio líquido-vapor (ELV). Considere um par de líquidos parcialmente miscíveis com temperatura crítica superior. Dependendo da pressão, podemos ter a junção de dois diagramas já vistos: o do ELL e o do ELV com formação de azeótropo.
Miscibilidade antes da Ebulição
Primeiro, avaliemos o sistema que, ao ser aquecido, torna-se homogêneo antes de ferver. O diagrama de fases correspondente é mostrado na figura abaixo.
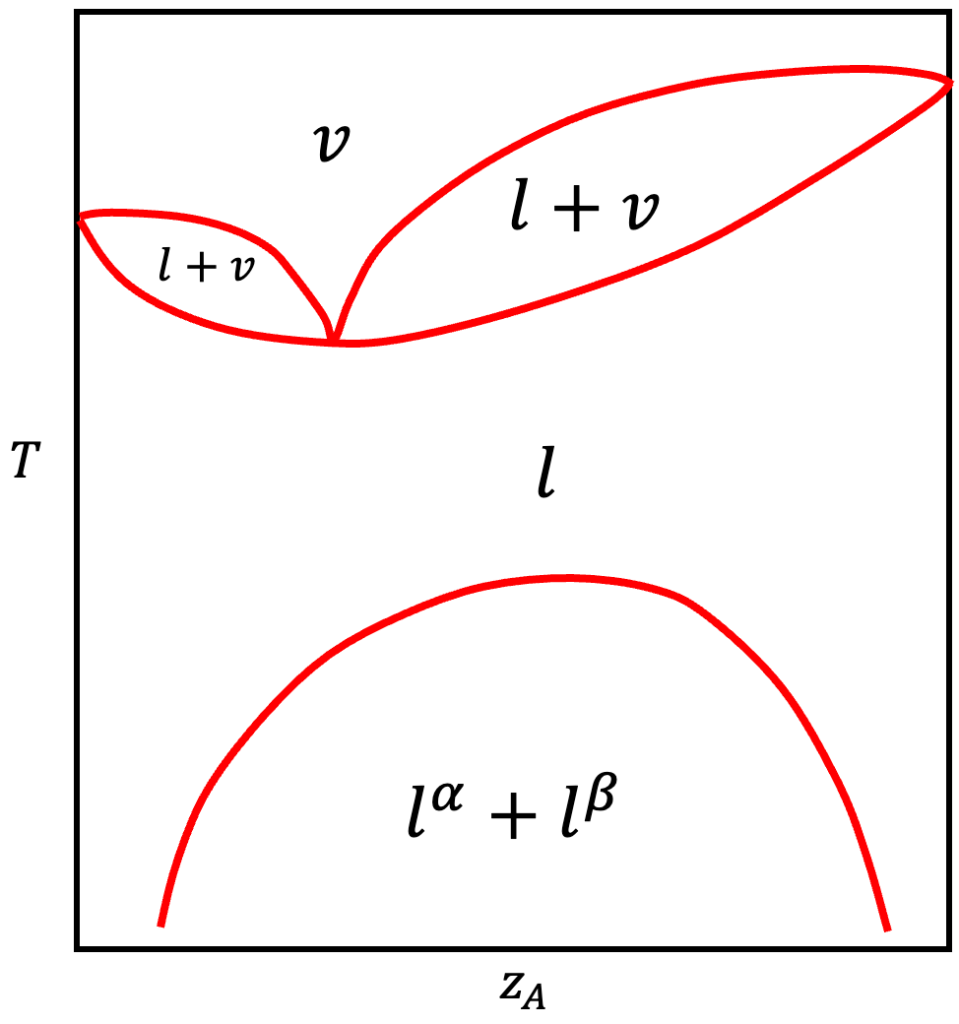
Não há muito o que discutir sobre a destilação fracionada de líquidos com esse comportamento porque, se estivermos na região ![]() e aquecermos o sistema, ele se tornará homogêneo e, depois, ocorrerá a destilação fracionada de uma solução, como discutimos no tópico de ELV. Certamente será o processo culminará na obtenção do azeótropo, como citamos na aula de ELV.
e aquecermos o sistema, ele se tornará homogêneo e, depois, ocorrerá a destilação fracionada de uma solução, como discutimos no tópico de ELV. Certamente será o processo culminará na obtenção do azeótropo, como citamos na aula de ELV.
Ebulição antes da Miscibilidade
Outra possibilidade ocorre quando o sistema pode entrar em ebulição antes de se tornar homogêneo. O diagrama de fases correspondente é mostrado na figura abaixo. Repare que ele é o equivalente ao anterior, pela aproximação das duas regiões (superior e inferior) até se interceptarem.
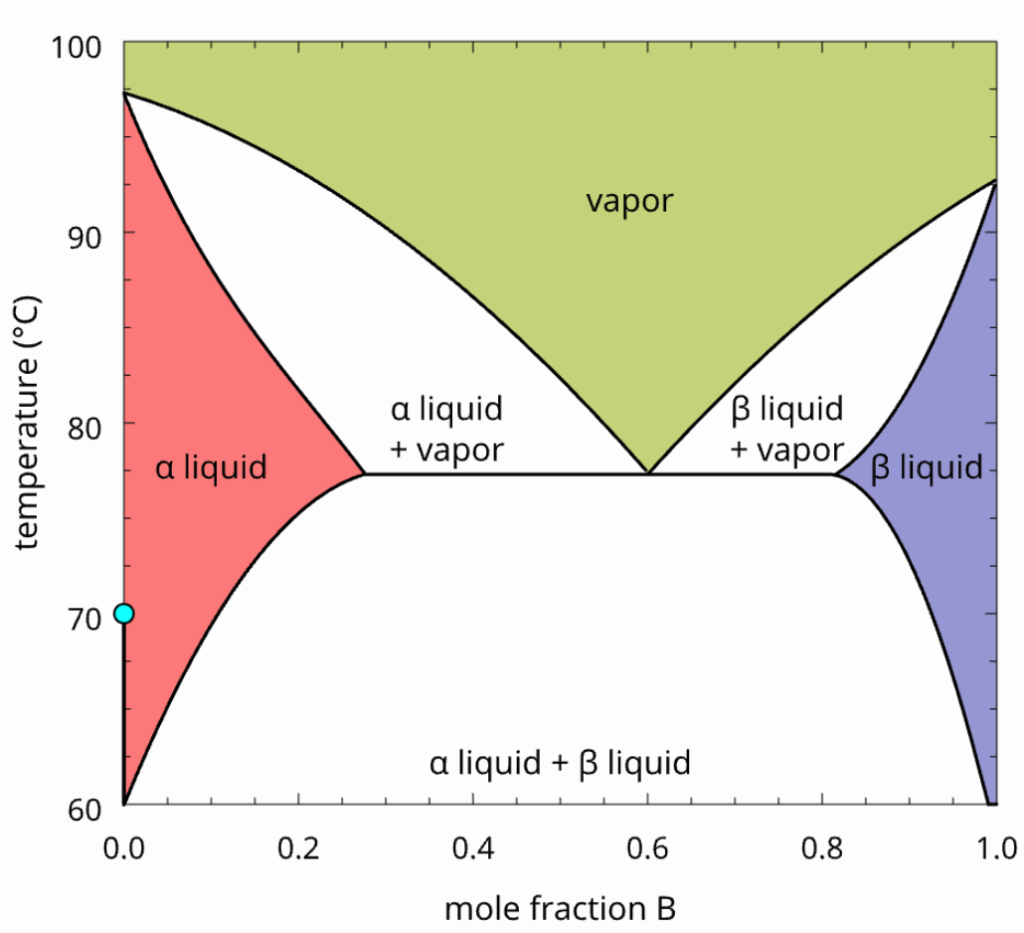
Vamos, primeiro, nos concentrar no aquecimento do sistema descrito pelo ponto abaixo. Quando a temperatura aumenta, teremos a miscibilidade dos líquidos. Não estranhe isso (pois citamos que o sistema ferve antes de tornar-se mnofásico), pois esse diagrama é referente à misturas de líquidos que podem tornar-se homogêneos antes de ferver, mas isso depende da composição.

A solução formada pelo aquecimento do sistema da figura acima é representado pelo ponto abaixo.
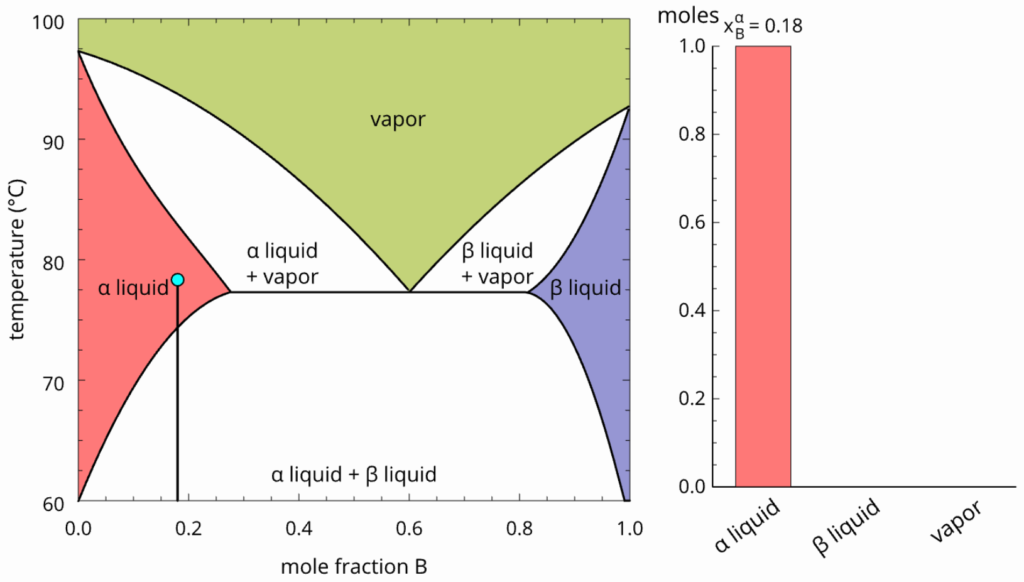
Ao continuar o aquecimento, chegaremos ao ponto de bolha, onde teremos o equilíbrio entre o líquido com composição global e o vapor com composição dada pela linha de amarração:
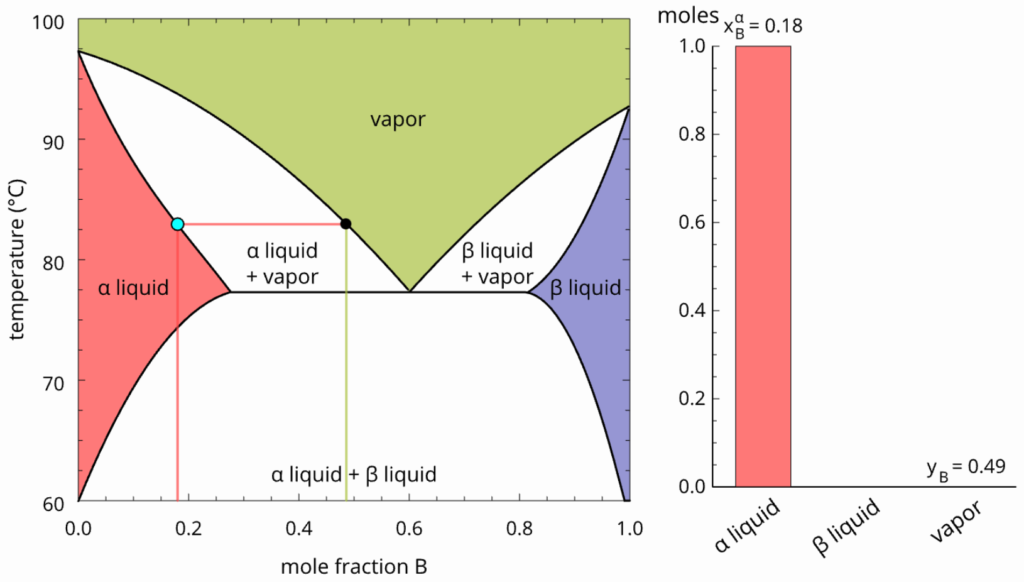
O aquecimento desse sistema só vai formar mais vapor e variar a composição das fases até atingir o último ponto da região bifásica, onde quase todo o sistema é um vapor com composição global e resta uma gota de líquido.
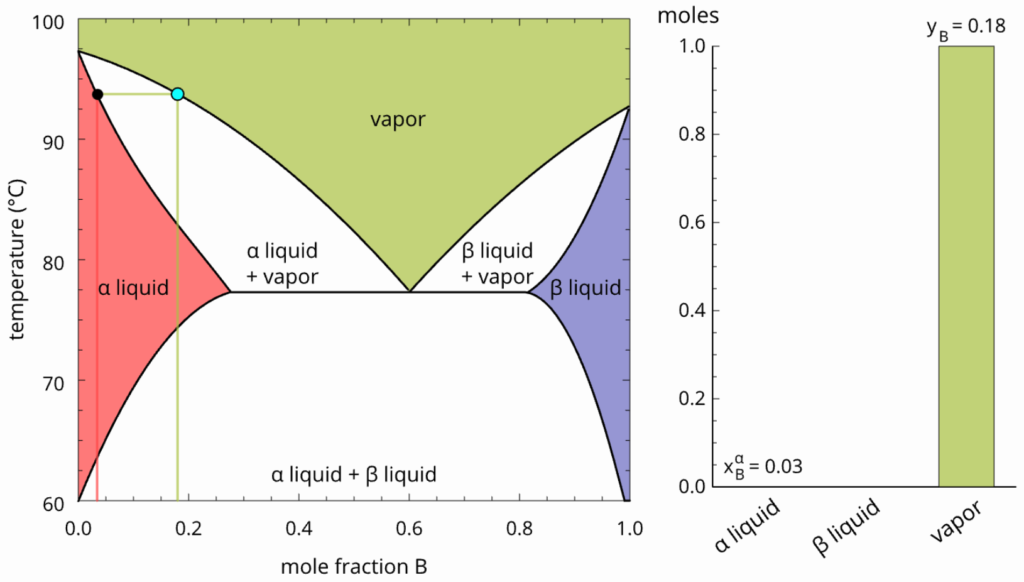
Aquecimento adicional só irá aumentar a energia cinética das moléculas do vapor.
Se, por outro lado, aquecermos o sistema descrito pelo ponto abaixo:

O comportamento é diferente do último caso. Ao invés de se tornar homogêneo, o sistema bifásico entra em ebulição, formando um único vapor (porque gases são sempre miscíveis) com composição dada pela linha de amarração, mostrada na figura abaixo. Perceba que ela passa por 3 pontos: a extremidade à esquerda fornece a composição do líquido ![]() ; a extremidade à direita fornece a composição do líquido
; a extremidade à direita fornece a composição do líquido ![]() ; e o ponto central fornece a composição do vapor. Esta linha de amarração só ocorre nessa temperatura específica e em uma faixa restrita de composições e, como representa o equilíbrio de dois líquidos com um vapor, todos os pontos dessa linha de amarração descreverão equilíbrios líquido-líquido-vapor (ELLV). No exemplo da figura, as composições do ELLV são
; e o ponto central fornece a composição do vapor. Esta linha de amarração só ocorre nessa temperatura específica e em uma faixa restrita de composições e, como representa o equilíbrio de dois líquidos com um vapor, todos os pontos dessa linha de amarração descreverão equilíbrios líquido-líquido-vapor (ELLV). No exemplo da figura, as composições do ELLV são ![]() ,
, ![]() e
e ![]() .
.
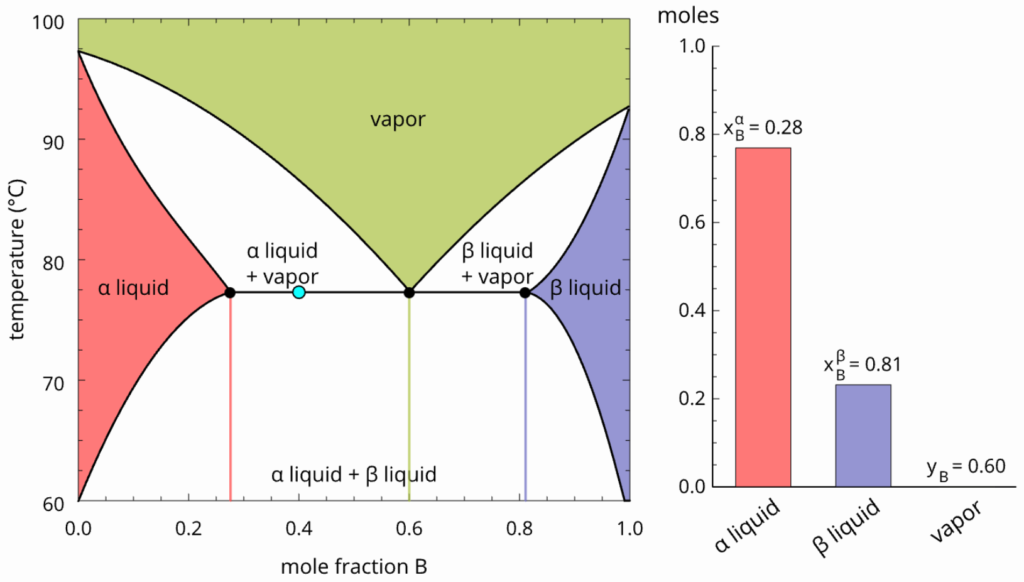
Se o aquecimento continuar, as composições das fases líquida e vapor se alteram até tocar a linha superior, onde existirá apenas uma gota de líquido e o vapor terá a composição global.
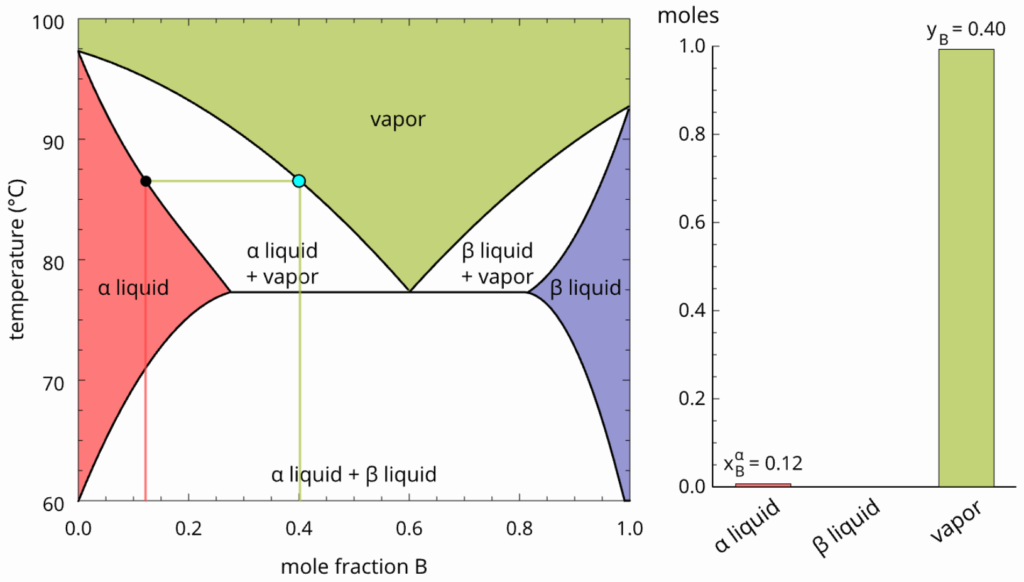
E o aquecimento adicional só aumentará a energia cinética das moléculas do vapor. Fenômenos exatamente equivalentes ocorrem se aquecermos o líquido de composição ![]() , só que com a “orelha” à direita (semelhante ao que acabamos de descrever). Se aquecermos um líquido descrito por um ponto na região “
, só que com a “orelha” à direita (semelhante ao que acabamos de descrever). Se aquecermos um líquido descrito por um ponto na região “![]() liquid”, ele terá o comportamento semelhante ao descrito para “
liquid”, ele terá o comportamento semelhante ao descrito para “![]() -liquid”.
-liquid”.
A destilação merece atenção especial. Se aquecermos o líquido descrito pelo ponto abaixo, o vapor formado no ELLV pode ser recolhido. Diferente do que foi abordado no ELV (onde deixávamos a temperatura aumentar acima do ponto de bolha para obter mais vapor), aqui no ELLV recolhemos o vapor na temperatura a linha de amarração do ELLV mesmo. Não pense que isso seria uma desvantagem porque só se formaria uma bolha de vapor, pois nessa linha de amarração a regra da alavanca não se aplica.
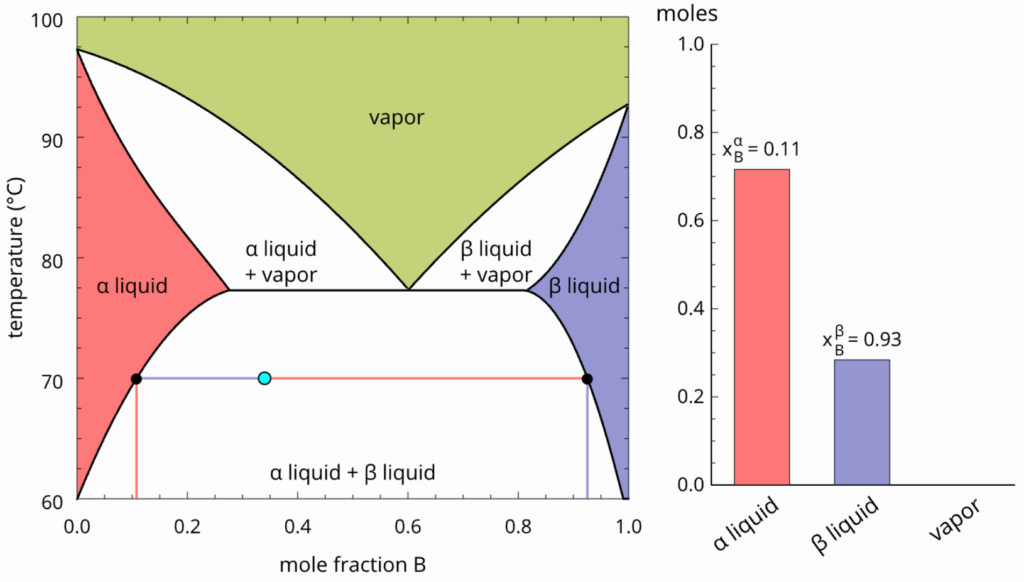
O vapor formado pode ser resfriado em um sistema heterogêneo cuja composição global é dada pelo ponto abaixo.
O reaquecimento desse sistema heterogêneo formará um vapor com mesma composição do líquido, ou seja, estamos diante de um azeótropo heterogêneo ou heteroazeótropo.
Exercícios
1) Anilina, ![]() e hexano formam misturas líquido-líquido parcialmente miscíveis a temperaturas abaixo de
e hexano formam misturas líquido-líquido parcialmente miscíveis a temperaturas abaixo de ![]() . Quando
. Quando ![]() de anilina e
de anilina e ![]() de hexano são misturados a uma temperatura de
de hexano são misturados a uma temperatura de ![]() , duas fases líquidas separadas são formadas, com frações molares de anilina de
, duas fases líquidas separadas são formadas, com frações molares de anilina de ![]() e
e ![]() . Determine o número de mol de cada componente em cada fase.
. Determine o número de mol de cada componente em cada fase.
Resposta
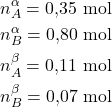
Resolução
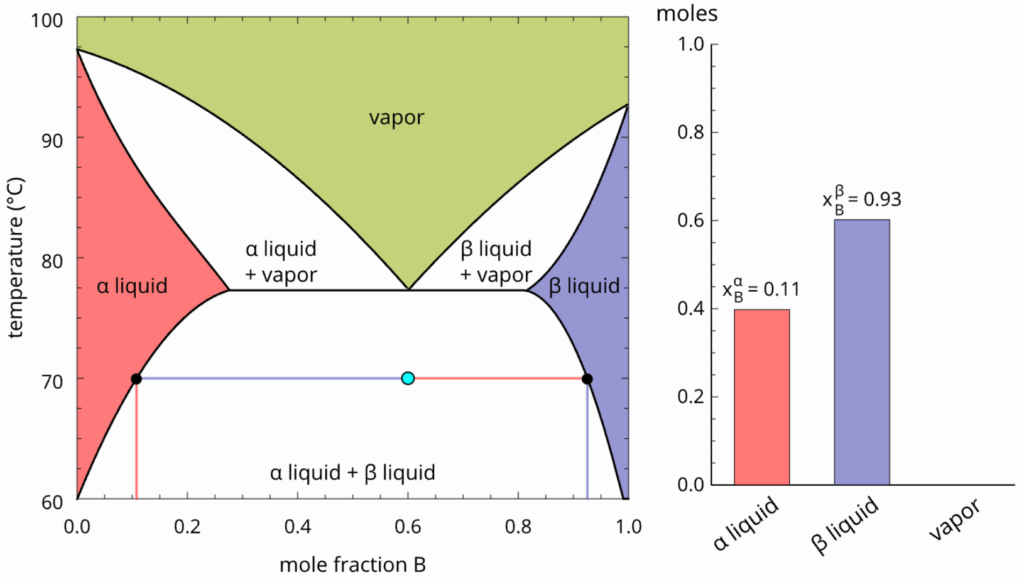
2) A figura mostra o diagrama de fases para etanol e dodecano.

a) Se misturarmos ![]() de cada componente a
de cada componente a ![]() , quais são as composições das fases em equilíbrio?
, quais são as composições das fases em equilíbrio?
b) Calcule o número de mols de cada fase.
c) Calcule a distribuição de A e B em cada fase.
d) Quanto de etanol temos que adicionar para que a composição global aumente para ![]() ?
?
e) Essa adição muda a composição das fases?
f) Calcule os números de mols em cada fase.
g) Calcule a distribuição de A e B em cada fase.
h) Quanto vale a temperatura crítica superior?
Resposta
a) O ponto que representa o sistema está em uma região bifásica e a composição de cada fase é dada pela linha de amarração. A primeira fase líquida tem composição aproximadamente ![]() e a segunda fase líquida tem composição
e a segunda fase líquida tem composição ![]() .
.
b)
![]()
![]()
c)
![]()
![]()
![]()
![]()
d) ![]()
e) Não muda. A fase líquida 2 fica mais abundante em número de mols, mas com a mesma composição inicial, assim como a fase líquida 1. Com a adição, as moléculas se redistribuem para manter a composição constante.
f)
![]()
![]()
g)
![]()
![]()
![]()
Resolução
3) Fenol e ![]() -naftol formam uma mistura binária de líquidos parcialmente miscíveis, cujo diagrama de fases é mostrado a seguir.
-naftol formam uma mistura binária de líquidos parcialmente miscíveis, cujo diagrama de fases é mostrado a seguir.
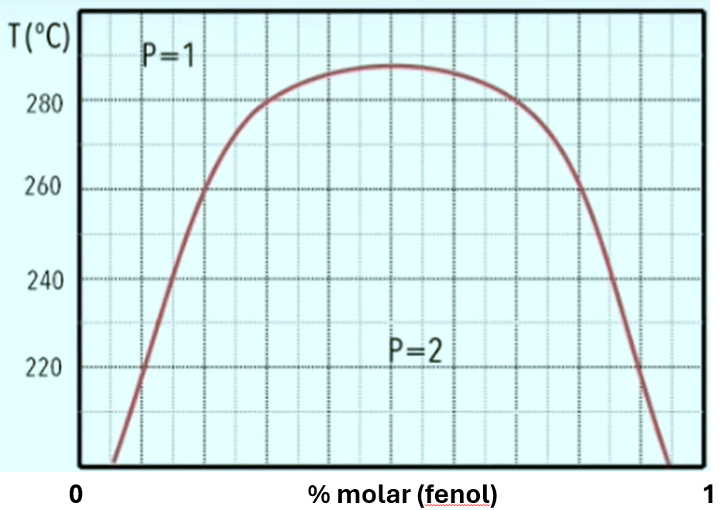
Para uma mistura formada por ![]() de fenol e
de fenol e ![]() de
de ![]() -naftol, determine:
-naftol, determine:
a) As composições da fase rica em fenol e da fase rica em ![]() -naftol a
-naftol a ![]() .
.
b) A abundância de cada fase, em ![]() .
.
c) A distribuição de cada componente do sistema, em ![]() .
.
d) A temperatura na qual a fase rica em ![]() -naftol se transforma em uma fase com
-naftol se transforma em uma fase com ![]() molar de fenol.
molar de fenol.
e) Quanto vale a temperatura consoluta superior?
Resposta
a) ![]() e
e ![]() .
.
b)
![]()
![]()
c)
![]()
![]()
![]()
![]()
d)
e)
Resolução
4) Considere o diagrama de fases a seguir, correspondente ao equilíbrio líquido-líquido entre o 2-butoxietanol (1) e a água (2).

a) Descreva o sistema formado ao misturarmos ![]() de 2-butoxietanol com
de 2-butoxietanol com ![]() de água em
de água em ![]() .
.
b) Descreva as alterações sofridas por este sistema se for resfriado.
c) Justifique a existência da temperatura consoluta inferior do ponto de vista microscópico.
Resposta
a) Tem-se um sistema bifásico, sendo uma das fases uma solução aquosa saturada do álcool, com fração molar aproximadamente ![]() em álcool e a outra uma solução alcoólica saturada de água, com fração molar aproximadamente
em álcool e a outra uma solução alcoólica saturada de água, com fração molar aproximadamente ![]() em água.
em água.
b) O resfriamento até aproximadamente ![]() homogeiniza o sistema.
homogeiniza o sistema.
c) Esse par de componentes pode interagir por meio de ligações de hidrogênio que são favorecidas quando o movimento térmico diminui e a solubilidade aumenta com o resfriamento.
Resolução
5) Considere o diagrama de fases a seguir, correspondente ao equilíbrio líquido-líquido entre água (A) e n-butil-éter-etilenoglicol (B).
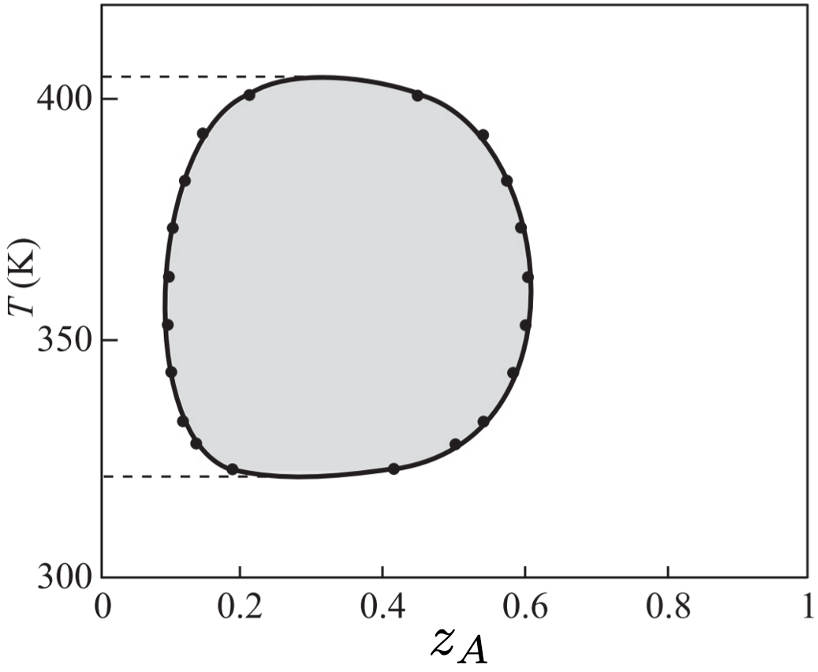
a) Para qual faixa de porcentagens molares de n-butil-éter-etilenoglicol é impossível obter um sistema líquido-líquido heterogêneo a ![]() ?
?
b) A ![]() , se misturarmos
, se misturarmos ![]() de B com
de B com ![]() de A, qual é a distribuição de cada componente em cada fase? Expresse em número de mols.
de A, qual é a distribuição de cada componente em cada fase? Expresse em número de mols.
Resposta
a) O sistema é sempre homogêneo quando ![]() .
.
b)
![]()
![]()
![]()
![]()
Resolução
6) Observa-se que a destilação a vapor do clorobenzeno ocorre a uma temperatura de ![]() quando a pressão é de
quando a pressão é de ![]() . Assumindo a imissibilidade completa desses líquidos, calcule a massa de clorobenzeno em
. Assumindo a imissibilidade completa desses líquidos, calcule a massa de clorobenzeno em ![]() de destilado. A pressão de vapor da água a
de destilado. A pressão de vapor da água a ![]() é de
é de ![]() .
.
Resposta
![]()
Gabarito
7) Uma solução de um soluto P em água foi agitada com um pouco de benzeno, e as concentrações de P em ambos os solventes foram medidas. A concentração de P na água foi de ![]() e sua concentração em benzeno foi de
e sua concentração em benzeno foi de ![]() . Calcule o coeficiente de partição de P entre benzeno e água. Interprete o resultado do ponto de vista das interações intermoleculares.
. Calcule o coeficiente de partição de P entre benzeno e água. Interprete o resultado do ponto de vista das interações intermoleculares.
Resposta
![]()
Resolução
8) Uma solução de iodo em tetraclorometano, a ![]() foi agitada com água até que o equilíbrio fosse estabelecido e, em seguida, as duas camadas foram deixadas se separar. Uma amostra de
foi agitada com água até que o equilíbrio fosse estabelecido e, em seguida, as duas camadas foram deixadas se separar. Uma amostra de ![]() da camada orgânica inferior foi titulada com solução de tiossulfato de sódio de
da camada orgânica inferior foi titulada com solução de tiossulfato de sódio de ![]() até que a cor do iodo fosse removida. Foi necessário
até que a cor do iodo fosse removida. Foi necessário ![]() de solução de tiossulfato de sódio.
de solução de tiossulfato de sódio. ![]() da camada aquosa foi titulada com solução de tiossulfato de sódio de
da camada aquosa foi titulada com solução de tiossulfato de sódio de ![]() . Neste caso,
. Neste caso, ![]() da solução de tiossulfato de sódio foi necessária para remover a cor do iodo. Calcule o coeficiente de partição do iodo entre tetraclorometano e água.
da solução de tiossulfato de sódio foi necessária para remover a cor do iodo. Calcule o coeficiente de partição do iodo entre tetraclorometano e água.
Dado:![]()
Resposta
![]()
Resolução
9) A figura a seguir é o diagrama de fases medido experimentalmente para misturas de água e butan-1-ol.
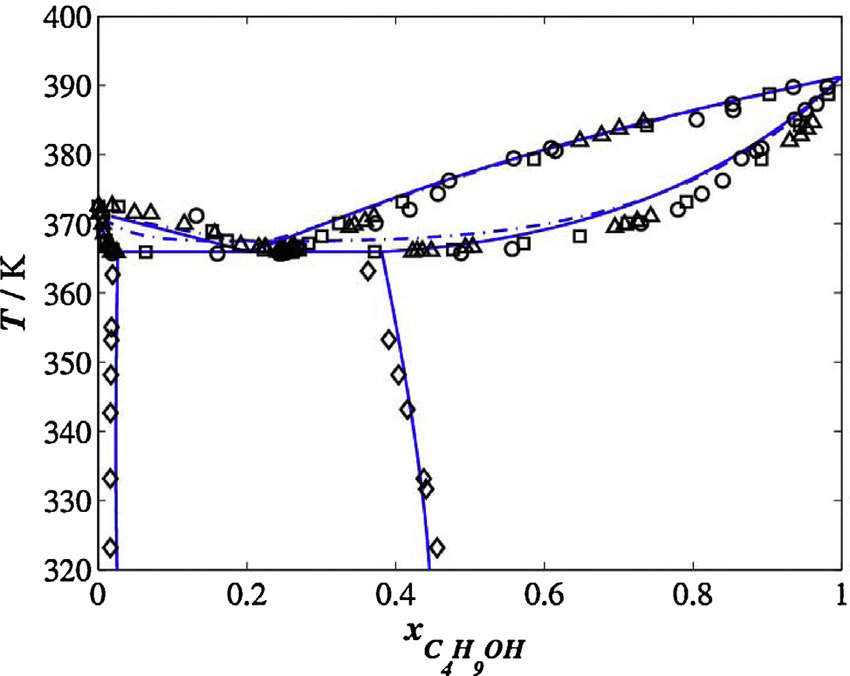
a) Qual é a temperatura azeotrópica?
b) Esse azeótropo é homogêneo ou heterogêneo?
c) Descreva as fases em equilíbrio em uma mistura de ![]() do álcool e
do álcool e ![]() de água, aquecida até
de água, aquecida até ![]() .
.
d) Qual é a solubilidade aproximada de butan-1-ol em água (em termos de frações molares) na temperatura de ![]() ?
?
e) Quais são as temperaturas de ebulição dos líquidos puros?
