O Potencial Químico (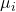 )
)
Vamos relembrar as equações de Gibbs para ![]() ,
, ![]() ,
, ![]() e
e ![]() .
.
(1) 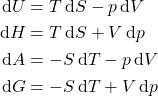
O que nos informa que, por exemplo, ![]() só pode variar, quando
só pode variar, quando ![]() e
e ![]() variam. Porém, essas equações não levam em consideração variações na composição do sistema, seja por entrada/saída de matéria (se o sistema for aberto), por reações químicas que podem ocorrer ou até por transferência de matéria entre fases (sólida, líquida, vapores,…). Dessa forma, podemos estender as equações 1, considerando a dependência das funções de estado com o número de mols, como mostrado na equação 2.
variam. Porém, essas equações não levam em consideração variações na composição do sistema, seja por entrada/saída de matéria (se o sistema for aberto), por reações químicas que podem ocorrer ou até por transferência de matéria entre fases (sólida, líquida, vapores,…). Dessa forma, podemos estender as equações 1, considerando a dependência das funções de estado com o número de mols, como mostrado na equação 2.
(2) 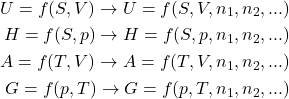
Assim, caso o número de mols dos componentes ![]() varie em
varie em ![]() ,
, ![]() , …, isso causará variações em
, …, isso causará variações em ![]() ,
, ![]() ,
, ![]() e
e ![]() . Para
. Para ![]() , podemos dizer que sua variação é dada pela equação 3.
, podemos dizer que sua variação é dada pela equação 3.
(3) ![]()
Vimos, no último tópico, que as duas primeiras derivadas parciais são ![]() e
e ![]() . Então, a equação 3 pode ser reescrita como mostrado na equação 4.
. Então, a equação 3 pode ser reescrita como mostrado na equação 4.
(4) ![]()
É importante não perder de vista que as equações descritas até aqui se aplicam à processos reversíveis, pois é a condição de ![]() . Porém, podemos aplicá-las em processos irreversíveis que conectem os mesmos estados inicial e final, uma vez que variações de funções de estado independem do caminho.
. Porém, podemos aplicá-las em processos irreversíveis que conectem os mesmos estados inicial e final, uma vez que variações de funções de estado independem do caminho.
As derivadas remanescentes na equação 4 nos levam à como ![]() varia quando o
varia quando o ![]() ,
, ![]() , … variam. Elas são as definições de potencial químico. Simplificadamente, o potencial químico
, … variam. Elas são as definições de potencial químico. Simplificadamente, o potencial químico ![]() mede a mudança na energia livre de Gibbs do sistema devido à variação isotérmica e isobárica do número de mols do participante
mede a mudança na energia livre de Gibbs do sistema devido à variação isotérmica e isobárica do número de mols do participante ![]() , como mostrado na equação 5.
, como mostrado na equação 5.
(5) ![]()
Assim, a mudança em ![]() mostrada na equação 4 pode ser reescrita como mostrado na equação 6.
mostrada na equação 4 pode ser reescrita como mostrado na equação 6.
(6) ![]()
Essa equação é de fundamental importância e é aplicável também a sistemas fechados nos quais a composição (![]() ) muda por transições de fase ou por reações químicas ocorrendo. A equação 6 cobre, ainda, sistemas abertos.
) muda por transições de fase ou por reações químicas ocorrendo. A equação 6 cobre, ainda, sistemas abertos.
Estamos citando ![]() o tempo todo, mas podemos estender a aplicação do potencial químico para
o tempo todo, mas podemos estender a aplicação do potencial químico para ![]() :
:
(7) 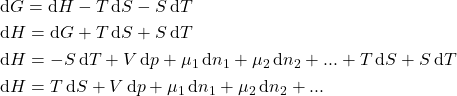
Ou para ![]() . Como
. Como ![]()
(8) 
Ou para ![]() . Como
. Como ![]() :
:
(9) 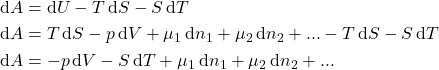
Assim, em resumo, as equações de Gibbs para ![]() ,
, ![]() ,
, ![]() e
e ![]() podem ser escritas como na equação 10.
podem ser escritas como na equação 10.
(10) 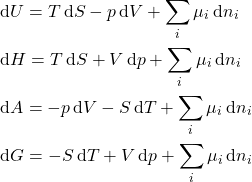
Ou seja, o potencial químico apresenta um significado mais amplo do que simplesmente quantificar a dependência isobárica e isotérmica de ![]() com a composição
com a composição ![]() , mas, também, a variação de
, mas, também, a variação de ![]() ,
, ![]() e
e ![]() com a composição. Só atente para o fato de que, para essas últimas funções de estado, a condição é diferente. Para
com a composição. Só atente para o fato de que, para essas últimas funções de estado, a condição é diferente. Para ![]() , por exemplo,
, por exemplo, ![]() nos fornece o quanto
nos fornece o quanto ![]() varia isentrópica e isocoricamente (
varia isentrópica e isocoricamente (![]() e
e ![]() fixos) com a composição
fixos) com a composição ![]() . Para
. Para ![]() , por exemplo,
, por exemplo, ![]() nos fornece o quanto
nos fornece o quanto ![]() varia isentrópica e isobaricamente (
varia isentrópica e isobaricamente (![]() e
e ![]() fixos) com a composição
fixos) com a composição ![]() . Para
. Para ![]() , por exemplo,
, por exemplo, ![]() nos fornece o quanto
nos fornece o quanto ![]() varia isocórica e isotermicamente (
varia isocórica e isotermicamente (![]() e
e ![]() fixos) com a composição
fixos) com a composição ![]() . Em resumo:
. Em resumo:
(11) 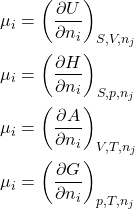
Potencial Químico e Equilíbrio Material
É comum, em termodinâmica, discutirmos a entrada ou saída de partículas em uma fase, uma porção homogênea do sistema, com propriedades físicas constantes em toda a sua extensão. As fases são comumente simbolizadas por letras gregas ![]() ,
, ![]() , etc. Quando uma quantidade infinitesimal de matéria
, etc. Quando uma quantidade infinitesimal de matéria ![]() migra (a
migra (a ![]() e
e ![]() fixos) de uma fase para outra (
fixos) de uma fase para outra (![]() , por exemplo), a variação infinitesimal de
, por exemplo), a variação infinitesimal de ![]() na fase
na fase ![]() é dada por
é dada por ![]() e, para a fase
e, para a fase ![]() ,
, ![]() , de modo que o
, de modo que o ![]() do sistema inteiro varia de:
do sistema inteiro varia de:
(12) ![]()
Ou, de forma mais geral, para quaisquer fases ![]() e componentes
e componentes ![]() presentes:
presentes:
(13) ![]()
Como a notação de somatória pode parecer, muitas vezes, confusa, a equação 13, aplicada ao exemplo de ![]() e
e ![]() sendo transferidos, simultaneamente, entre as fases
sendo transferidos, simultaneamente, entre as fases ![]() e
e ![]() é:
é:
(14) ![]()
Por exemplo, para água e etanol, nas fases líquida e vapor, temos que:
(15) ![]()
Dessa forma, a variação total de ![]() em um sistema com várias fases, sem ocorrência de reação química é dada pela equação 16, onde
em um sistema com várias fases, sem ocorrência de reação química é dada pela equação 16, onde ![]() é a entropia da fase e
é a entropia da fase e ![]() é o volume da fase.
é o volume da fase.
(16) ![]()
De modo que o potencial químico de um componente ![]() na fase
na fase ![]() é dado pela equação 17.
é dado pela equação 17.
(17) ![]()
Quando duas fases estão em equilíbrio a uma certa temperatura ![]() fixa e uma certa pressão
fixa e uma certa pressão ![]() fixa, temos que:
fixa, temos que:
(18) 
Aplicando esses valores à equação 16, podemos escrever a equação 19.
(19) ![]()
A equação 19 extrapola o contexto do equilíbrio de fases em ![]() e
e ![]() constantes. Ela também vale para sistemas em equilíbrio independente da forma como ele foi atingido. Para
constantes. Ela também vale para sistemas em equilíbrio independente da forma como ele foi atingido. Para ![]() e
e ![]() constantes, é
constantes, é ![]() (e não
(e não ![]() ) que descreve espontaneidade e equilíbrio, mas a equação 19 continua válida para
) que descreve espontaneidade e equilíbrio, mas a equação 19 continua válida para ![]() e
e ![]() constantes.
constantes.
Duas características importantes do potencial químico: ele é uma variável intensiva (porque ![]() e
e ![]() são extensivas) é, também, uma função de estado, pois
são extensivas) é, também, uma função de estado, pois ![]() também o é. Outro ponto que merece destaque é que a forma como definimos o potencial químico (equação 11) sugere que está relacionado a uma variação de
também o é. Outro ponto que merece destaque é que a forma como definimos o potencial químico (equação 11) sugere que está relacionado a uma variação de ![]() . O significado disso é que
. O significado disso é que ![]() pode existir em um sistema onde
pode existir em um sistema onde ![]() é ausente, pois ele trata da variação causada em uma hipotética adição de uma quantidade
é ausente, pois ele trata da variação causada em uma hipotética adição de uma quantidade ![]() de
de ![]() e não significa que esse
e não significa que esse ![]() já esteja lá.
já esteja lá.
A energia de Gibbs de um sistema puro formado por uma substância ![]() é
é ![]() . Assim, aplicando a equação 11:
. Assim, aplicando a equação 11:
(20) ![]()
E o potencial químico de uma substância pura é a sua energia de Gibbs molar. No entanto, para uma mistura, ![]() .
.
O Equilíbrio de Fases
Um equilíbrio de fases ocorre quando quando o potencial químico da mesma espécie é igual em duas fases diferentes. O equilíbrio líquido-vapor da água (![]() ) e o equilíbrio de solubilidade da glicose (
) e o equilíbrio de solubilidade da glicose (![]() ) são exemplos de equilíbrio de fases. Para o equilíbrio de
) são exemplos de equilíbrio de fases. Para o equilíbrio de ![]() entre as fases
entre as fases ![]() e
e ![]() , a equação 19 equivale a:
, a equação 19 equivale a:
(21) ![]()
Como a quantidade que sai da fase ![]() é a mesma que entra na fase
é a mesma que entra na fase ![]() , podemos escrever
, podemos escrever ![]() e
e ![]() , podemos escrever:
, podemos escrever:
(22) 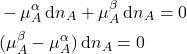

Como ![]() não pode nulo, temos que a condição de equilíbrio de fases é:
não pode nulo, temos que a condição de equilíbrio de fases é:
(23) ![]()
Reforçando que a igualdade dos potenciais químicos é a condição do equilíbrio de fases. Enquanto o equilíbrio não é atingido, matéria flui da fase que tem maior potencial químico para a que possui menor potencial químico, minimizando ![]() . Antes do equilíbrio,
. Antes do equilíbrio, ![]() . Perceba que, assim como a diferença de temperatura é a força motriz para o fluxo espontâneo de calor, a diferença dos potenciais químicos é a força motriz para o fluxo espontâneo de matéria.
. Perceba que, assim como a diferença de temperatura é a força motriz para o fluxo espontâneo de calor, a diferença dos potenciais químicos é a força motriz para o fluxo espontâneo de matéria.
Só há uma exceção para essa regra. Imagine uma situação onde a substância ![]() está presente apenas em uma fase (
está presente apenas em uma fase (![]() , como ilustrado na figura abaixo). Mesmo que não exista
, como ilustrado na figura abaixo). Mesmo que não exista ![]() em
em ![]() ,
, ![]() é definido em ambas as fases (já citamos isso antes).
é definido em ambas as fases (já citamos isso antes).
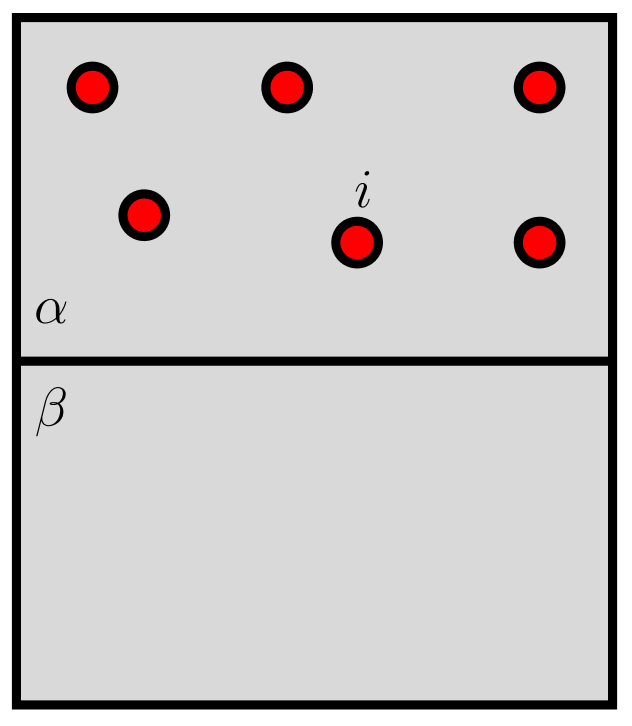
É claro que, se ![]() , ocorrerá transferência irreversível de matéria na direção
, ocorrerá transferência irreversível de matéria na direção ![]() . Porém, se
. Porém, se ![]() , não pode haver transferência de matéria porque
, não pode haver transferência de matéria porque ![]() não está em
não está em ![]() e o sistema está em equilíbrio mesmo que os potenciais químicos não sejam iguais. Então, quando
e o sistema está em equilíbrio mesmo que os potenciais químicos não sejam iguais. Então, quando ![]() está ausente em
está ausente em ![]() , a condição termodinâmica de equilíbrio é:
, a condição termodinâmica de equilíbrio é:
(24) ![]()
A Regra das Fases
Um sistema pode ter muitos componentes e muitas fases. Quanto mais complexo for um sistema, mais informações são necessárias para descrevê-lo. Por exemplo, para a água pura, líquida, a ![]() e
e ![]() , temos apenas um componente e uma fase. Para descrever esse sistema só precisamos dessas duas variáveis citadas: a pressão e a temperatura. Para uma solução de água e sacarose, por exemplo, temos dois componentes e precisamos saber, também, a concentração da sacarose.
, temos apenas um componente e uma fase. Para descrever esse sistema só precisamos dessas duas variáveis citadas: a pressão e a temperatura. Para uma solução de água e sacarose, por exemplo, temos dois componentes e precisamos saber, também, a concentração da sacarose.
O número de propriedades intensivas independentes necessárias para descrever o estado intensivo de um sistema é chamado de variância ou graus de liberdade (![]() ). Por “descrever o estado intensivo”, deve-se compreender “descrever o estado do sistema, exceto sua dimensão ou tamanho”. Perceba que a água líquida possui, então, dois graus de liberdade: a pressão e a temperatura. Nós só conseguimos descrever o estado da água líquida conhecendo essas duas propriedades.
). Por “descrever o estado intensivo”, deve-se compreender “descrever o estado do sistema, exceto sua dimensão ou tamanho”. Perceba que a água líquida possui, então, dois graus de liberdade: a pressão e a temperatura. Nós só conseguimos descrever o estado da água líquida conhecendo essas duas propriedades.
O nome liberdade vem do fato de que, para a água, por exemplo, podemos mudar sua temperatura para ![]() e a pressão para
e a pressão para ![]() e ela continuará líquida. Ou seja, a pressão e a temperatura podem variar de forma independente, mantendo o mesmo número de fases em equilíbrio. Por isso
e ela continuará líquida. Ou seja, a pressão e a temperatura podem variar de forma independente, mantendo o mesmo número de fases em equilíbrio. Por isso ![]() é, frequentemente, associado ao número de variáveis intensivas que podem ser manipuladas de forma independente, mantendo fixo o número de fases de um sistema. No caso da água, como podemos manipular ambas as variáveis intensivas (
é, frequentemente, associado ao número de variáveis intensivas que podem ser manipuladas de forma independente, mantendo fixo o número de fases de um sistema. No caso da água, como podemos manipular ambas as variáveis intensivas (![]() e
e ![]() ) mantendo uma fase, a variância é
) mantendo uma fase, a variância é ![]() .
.
Gibbs chegou a uma expressão que relaciona a variância ![]() de um sistema com o número de fases
de um sistema com o número de fases ![]() e o número de componentes
e o número de componentes ![]() (supondo que não ocorram reações e todas as espécies estejam em todas as fases.
(supondo que não ocorram reações e todas as espécies estejam em todas as fases.
![]() é função de
é função de ![]() ,
, ![]() e dos números de mols das
e dos números de mols das ![]() substâncias em cada fase
substâncias em cada fase ![]() (equação 10). Assim,
(equação 10). Assim, ![]() e
e ![]() são sempre necessárias e, para misturas, é necessário conhecer, também, a composição de cada componente em cada fase. Poderíamos pensar em número de mols, mas, na verdade, precisamos de propriedades intentivas para constuir
são sempre necessárias e, para misturas, é necessário conhecer, também, a composição de cada componente em cada fase. Poderíamos pensar em número de mols, mas, na verdade, precisamos de propriedades intentivas para constuir ![]() . Se dividirmos o número de mols de um participante
. Se dividirmos o número de mols de um participante ![]() qualquer na fase
qualquer na fase ![]() (
(![]() ) pelo número de mols total dessa fase (
) pelo número de mols total dessa fase (![]() ), obteremos a fração molar de
), obteremos a fração molar de ![]() nessa fase (que é a propriedade intensiva que procurávamos):
nessa fase (que é a propriedade intensiva que procurávamos):
(25) ![]()
Assim, para o sistema “água + etanol”, poderíamos pensar em seis variáveis intensivas: ![]() ,
, ![]() (óbvias),
(óbvias), ![]() ,
, ![]() ,
, ![]() e
e ![]() . Alguém poderia afirmar que a variância é seis, mas isso não está correto. A razão disso é que
. Alguém poderia afirmar que a variância é seis, mas isso não está correto. A razão disso é que ![]() , na verdade, só contabiliza variáveis independentes.
, na verdade, só contabiliza variáveis independentes.
Assim, podemos perceber que ![]() , ou seja,
, ou seja, ![]() e
e ![]() não são independentes. Se especificarmos
não são independentes. Se especificarmos ![]() , sabemos, pela relação matemática,
, sabemos, pela relação matemática, ![]() e basta conhecermos uma delas. Dessa forma, uma relação matemática remove um grau de liberdade, pois torna-o desnecessário. Revisite os últimos parágrafos caso não tenha entendido, pois são fundamentais para uma compreensão mais clara do conceito de
e basta conhecermos uma delas. Dessa forma, uma relação matemática remove um grau de liberdade, pois torna-o desnecessário. Revisite os últimos parágrafos caso não tenha entendido, pois são fundamentais para uma compreensão mais clara do conceito de ![]() .
.
Imagine que aumentamos a temperatura da água líquida pura até seu ponto de ebulição, onde o líquido e o vapor estejam em equilíbrio. A ![]() de pressão, essa temperatura é de
de pressão, essa temperatura é de ![]() . Para manter as duas fases em equilíbrio, dessa vez, não podemos variar
. Para manter as duas fases em equilíbrio, dessa vez, não podemos variar ![]() e
e ![]() o quanto quisermos, pois, para maiores temperaturas, apenas o vapor está presente e, para menores temperatuas, apenas o líquido está presente. Que relação matemática nos fez perder mais um grau de liberdade? Justamente a condição de equilíbrio de fases:
o quanto quisermos, pois, para maiores temperaturas, apenas o vapor está presente e, para menores temperatuas, apenas o líquido está presente. Que relação matemática nos fez perder mais um grau de liberdade? Justamente a condição de equilíbrio de fases: ![]() .
.
A expressão alcançada por Gibbs foi obtida com base nos argumentos que seguem. Para ![]() componentes em
componentes em ![]() fases, temos, além de
fases, temos, além de ![]() e
e ![]() ,
, ![]() frações molares. Até agora o número de variáveis intensivas a serem descobertas é
frações molares. Até agora o número de variáveis intensivas a serem descobertas é ![]() , onde
, onde ![]() representa
representa ![]() e
e ![]() . Porém, a soma das frações molares é
. Porém, a soma das frações molares é ![]() em cada fase e, conhecendo
em cada fase e, conhecendo ![]() frações molares em cada fase, saberemos a última fração molar pelo “quanto falta para alcançar a unidade”. Assim, precisamos excluir
frações molares em cada fase, saberemos a última fração molar pelo “quanto falta para alcançar a unidade”. Assim, precisamos excluir ![]() variáveis intensivas dessa conta:
variáveis intensivas dessa conta: ![]() .
.
No entanto, como todos os ![]() componentes está em cada uma das
componentes está em cada uma das ![]() fases, podemos construir relações de igualdade do tipo
fases, podemos construir relações de igualdade do tipo ![]() . Para ilustrar isso de maneira mais simples, suponha que cada fase seja representada pelo vértice de um polígono com tantos lados quantos forem os números de fase. Para seis fases, por exemplo:
. Para ilustrar isso de maneira mais simples, suponha que cada fase seja representada pelo vértice de um polígono com tantos lados quantos forem os números de fase. Para seis fases, por exemplo:
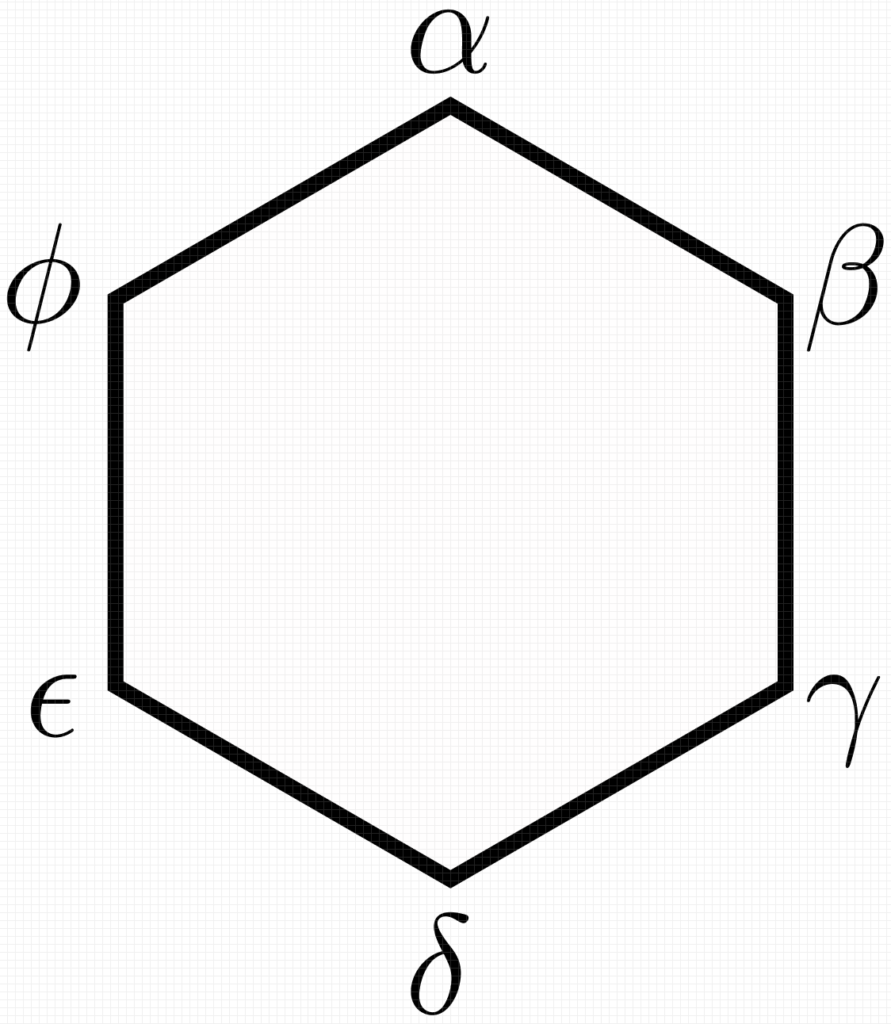
Assim, o componente ![]() apresenta potencial químico igual em cada fase e essas igualdades serão representadas por retas que conectem
apresenta potencial químico igual em cada fase e essas igualdades serão representadas por retas que conectem ![]() a cada uma das fases. Para esse polígono, podemos encontrar cinco retas, mostradas abaixo em vermelho.
a cada uma das fases. Para esse polígono, podemos encontrar cinco retas, mostradas abaixo em vermelho.
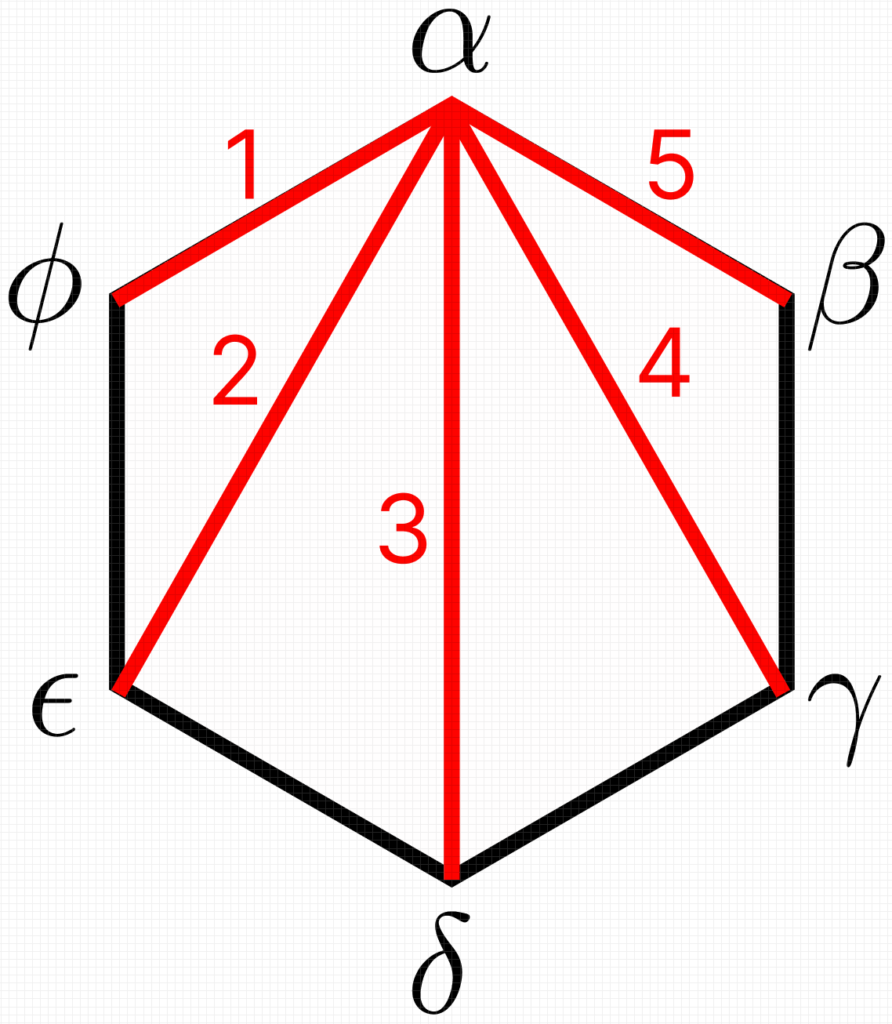
E, para o componente ![]() , temos
, temos ![]() relações de igualdade de potenciais químicos, nos permitindo eliminar
relações de igualdade de potenciais químicos, nos permitindo eliminar ![]() variáveis intensivas. Como temos
variáveis intensivas. Como temos ![]() componentes, podemos construir um hexágono como esse para cada componente e o número de variáveis intensivas removas será
componentes, podemos construir um hexágono como esse para cada componente e o número de variáveis intensivas removas será ![]() .
.
Dessa forma, tínhamos ![]() variáveis necessárias e, agora, teremos
variáveis necessárias e, agora, teremos ![]() . Após uma álgebra básica:
. Após uma álgebra básica:
![Rendered by QuickLaTeX.com \begin{align*}&F = (PC + 2) - (P) - [(P - 1)C]\\&F = PC + 2 - P - PC + C\\&\boxed{F = C - P + 2}\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-016d23cdee9441805b29ff5bdf768736_l3.png)
Que é a regra das fases de Gibbs. Perceba que, se removermos a restrição dos componentes estarem presentes em todas as fases não altera a regra das fases de Gibbs. Por exemplo, se um componente não está na fase ![]() , sua fração molar nessa frase não é mais necessária (perdemos um grau de liberdade), mas, também, o potencial químico dessa espécie não precisa ser igual ao das outras fases e eliminamos uma relação de igualdade. Assim:
, sua fração molar nessa frase não é mais necessária (perdemos um grau de liberdade), mas, também, o potencial químico dessa espécie não precisa ser igual ao das outras fases e eliminamos uma relação de igualdade. Assim:
![Rendered by QuickLaTeX.com \begin{align*}&F = (PC + 2) - (P - 1) - [(P - 1)C] - 1\\&F = PC + 2 - P + 1 - (P - 1)C - 1\\&F = PC + 2 - P + 1 - PC + C - 1\\&\boxed{F = C - P + 2}\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-f70cf46b5e33555e45d1986de89537ff_l3.png)
O Diagrama de Fases de Substâncias
Para a água líquida pura (![]() e
e ![]() ), o número de graus de liberdade é
), o número de graus de liberdade é ![]() e o sistema é dito bivariante, no sentido que podemos variar
e o sistema é dito bivariante, no sentido que podemos variar ![]() e
e ![]() e ainda teremos uma única fase no sistema. Para água no equilíbrio líquido-vapor (
e ainda teremos uma única fase no sistema. Para água no equilíbrio líquido-vapor (![]() e
e ![]() ), temos que
), temos que ![]() e o sistema é dito ser monovariante, de modo que só podemos mudar uma variável intensiva de forma independente mantendo duas fases em equilíbrio. Para água nos três estados de agregação em equilíbrio (
e o sistema é dito ser monovariante, de modo que só podemos mudar uma variável intensiva de forma independente mantendo duas fases em equilíbrio. Para água nos três estados de agregação em equilíbrio (![]() e
e ![]() ), temos
), temos ![]() , ou seja, o sistema é invariante e não podemos mudar nenhuma variável intensiva mantendo três fases em equilíbrio (este é o ponto triplo).
, ou seja, o sistema é invariante e não podemos mudar nenhuma variável intensiva mantendo três fases em equilíbrio (este é o ponto triplo).
Essas características estão resumidas de forma muito mais fácil de acompanhar em um diagrama de fases, um gráfico que mostra que fases são mais estáveis (menor valor de ![]() ) em cada região de valores de
) em cada região de valores de ![]() e
e ![]() . Parte do diagrama de fases da água é mostrado abaixo.
. Parte do diagrama de fases da água é mostrado abaixo.
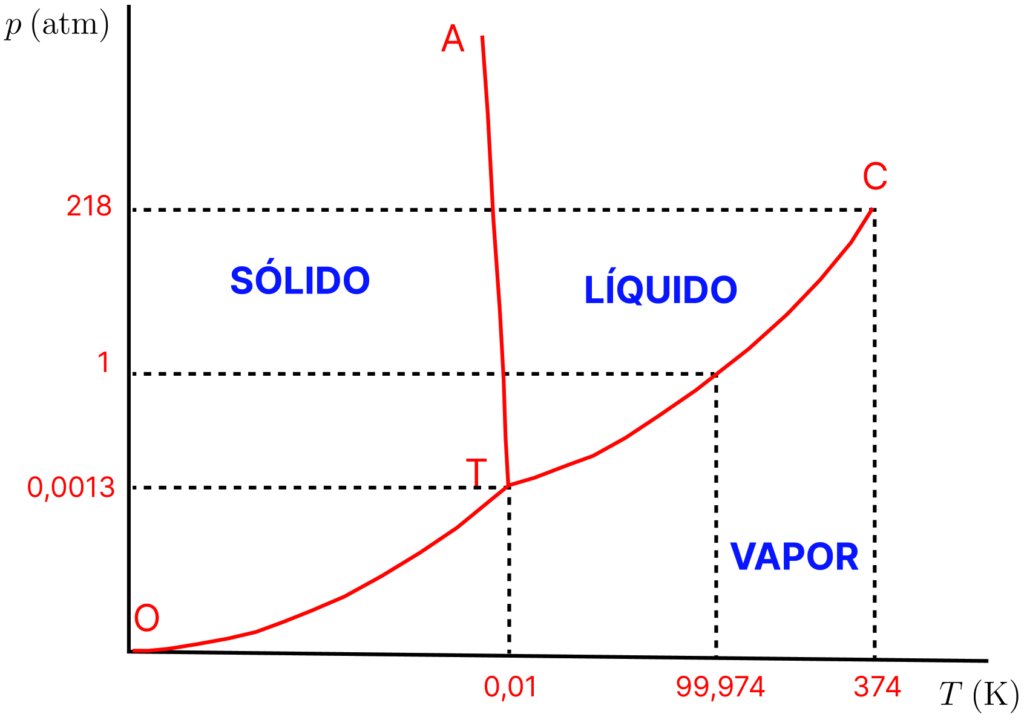
As áreas abertas são as regiões monofásicas, onde ![]() , o que é coerente com o fato de ser uma região bidimensional, onde podemos variar duas propriedades (
, o que é coerente com o fato de ser uma região bidimensional, onde podemos variar duas propriedades (![]() e
e ![]() ), mantendo uma fase em equilíbrio. Ao longo das curvas, temos duas fases em equilíbrio e
), mantendo uma fase em equilíbrio. Ao longo das curvas, temos duas fases em equilíbrio e ![]() , de forma que só temos a liberdade de escolher
, de forma que só temos a liberdade de escolher ![]() ou
ou ![]() e a outra será especificada pela linha. O fato de ser uma linha é coerente com um sistema monovariante. A figura mostra o ponto na linha TC. Ele indica que a água líquida e vapor estão em equilíbrio a
e a outra será especificada pela linha. O fato de ser uma linha é coerente com um sistema monovariante. A figura mostra o ponto na linha TC. Ele indica que a água líquida e vapor estão em equilíbrio a ![]() e
e ![]() . Esses valores são conhecidos como pressão de vapor (já comentarei sobre esse conceito) e a temperatura de ebulição. Assim, a curva TC nos fornece a pressão de vapor da água em função da temperatura e a temperatura de ebulição em função da pressão.
. Esses valores são conhecidos como pressão de vapor (já comentarei sobre esse conceito) e a temperatura de ebulição. Assim, a curva TC nos fornece a pressão de vapor da água em função da temperatura e a temperatura de ebulição em função da pressão.
O ponto T é o ponto triplo, representando o único sistema invariante, ou seja, ![]() e, nesse estado, os três estados de agregação estão, juntos, em equilíbrio. As condições do ponto triplo da água são
e, nesse estado, os três estados de agregação estão, juntos, em equilíbrio. As condições do ponto triplo da água são ![]() e
e ![]() (
(![]() ).
).
A curva TA fornece os pontos de fusão em cada pressão, ou seja, a temperatura na qual sólido e líquido estão em equilíbrio. Perceba que o ponto de fusão do gelo diminuir com o aumento da pressão, devido à inclinação decrescente da reta. Isso não ocorre com todas as substâncias e será comentado em mais detalhes futuramente.
Perceba que a água não pode sofrer sublimação em ![]() , uma vez que o ponto triplo ocorre abaixo dessa pressão. Para pressões abaixo do ponto triplo, a curva TO mostra como a pressão de vapor do sólido varia com a temperatura e, de acordo com a mecânica estatística, essa grandeza tende a zero quando
, uma vez que o ponto triplo ocorre abaixo dessa pressão. Para pressões abaixo do ponto triplo, a curva TO mostra como a pressão de vapor do sólido varia com a temperatura e, de acordo com a mecânica estatística, essa grandeza tende a zero quando ![]() , ou seja, a curva TO precisa cortar o diagrama de fases na origem.
, ou seja, a curva TO precisa cortar o diagrama de fases na origem.
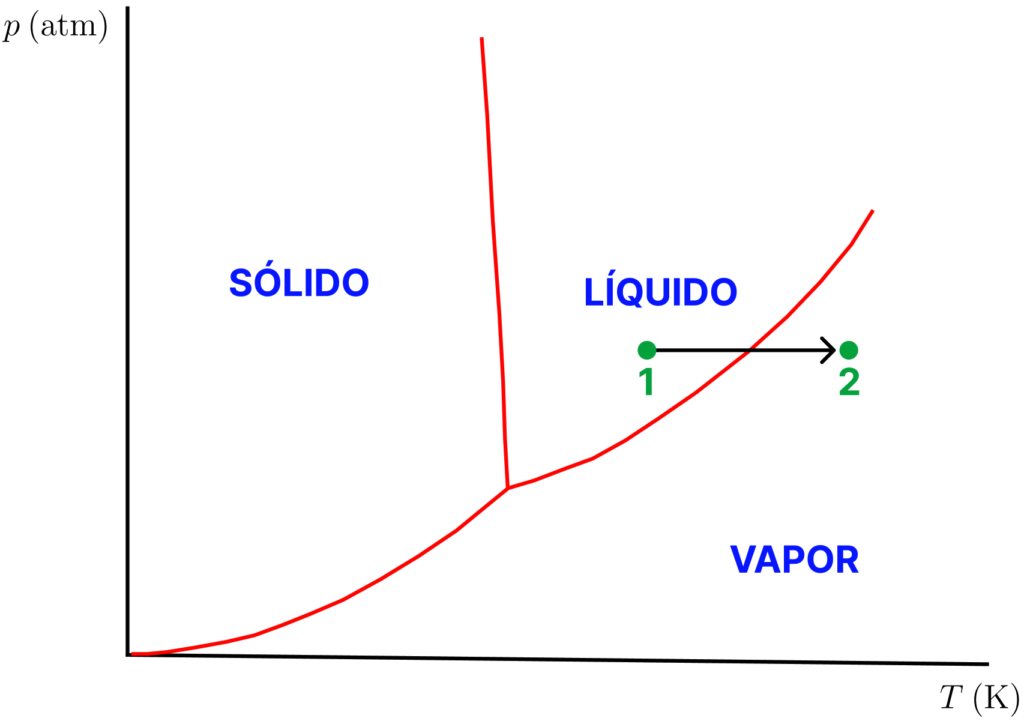
Imagine que estejamos em uma condição de ![]() e
e ![]() referente ao ponto 1 do diagrama abaixo. O líquido pode ser aquecido isobaricamente, como fazemos, por exemplo, com a água na panela. A temperatura atinge o ponto de ebulição quando o ponto 1 tocar a curva de equilíbrio líquido-vapor (LV) e a ebulição começa a ocorrer. A massa de líquido diminui enquanto a massa de vapor aumenta e estamos estagnados o ponto sobre a linha LV até que apenas vapor esteja presente. Aquecimento adicional nos levará até algo próximo do ponto 2. É óbvio que, se resfriamento for feito sobre o ponto 2, o processo inverso ocorrerá.
referente ao ponto 1 do diagrama abaixo. O líquido pode ser aquecido isobaricamente, como fazemos, por exemplo, com a água na panela. A temperatura atinge o ponto de ebulição quando o ponto 1 tocar a curva de equilíbrio líquido-vapor (LV) e a ebulição começa a ocorrer. A massa de líquido diminui enquanto a massa de vapor aumenta e estamos estagnados o ponto sobre a linha LV até que apenas vapor esteja presente. Aquecimento adicional nos levará até algo próximo do ponto 2. É óbvio que, se resfriamento for feito sobre o ponto 2, o processo inverso ocorrerá.
A Pressão de Vapor e a Ebulição
É comum discutirmos o fenômeno da ebulição apenas em termos de temperatura, no sentido que um líquido só entra em ebulição quando a sua temperatura atinge uma propriedade do próprio líquido: o ponto de ebulição, nas condições do experimento. No entanto, a compreensão da ebulição é mais profunda se tivermos o conhecimento da pressão de vapor e como essa grandeza varia com a temperatur ado líquido.
A pressão de vapor é a pressão exercida pelo vapor em equilíbrio com a fase condensada, a uma certa temperatura. Imagine um líquido, por exemplo, em um recipiente fechado com vácuo absoluto sobre sua superfície. Nesta situação, a pressão sobre a superfície do líquido é nula. Com o tempo, moléculas do líquido passam, espontaneamente, para o estado gasoso até que os potenciais químicos em ambas as fases se igualem e o equilíbrio LV é atingido: ![]() . A quantidade de vapor acima do líquido é, agora, fixa e exerce uma pressão chamada de pressão de vapor. A pressão de vapor da água, a
. A quantidade de vapor acima do líquido é, agora, fixa e exerce uma pressão chamada de pressão de vapor. A pressão de vapor da água, a ![]() , é
, é ![]() , mas obviamente, será maior quando a temperatura aumentar (o diagrama de fases mostra isso, na linha TC).
, mas obviamente, será maior quando a temperatura aumentar (o diagrama de fases mostra isso, na linha TC).
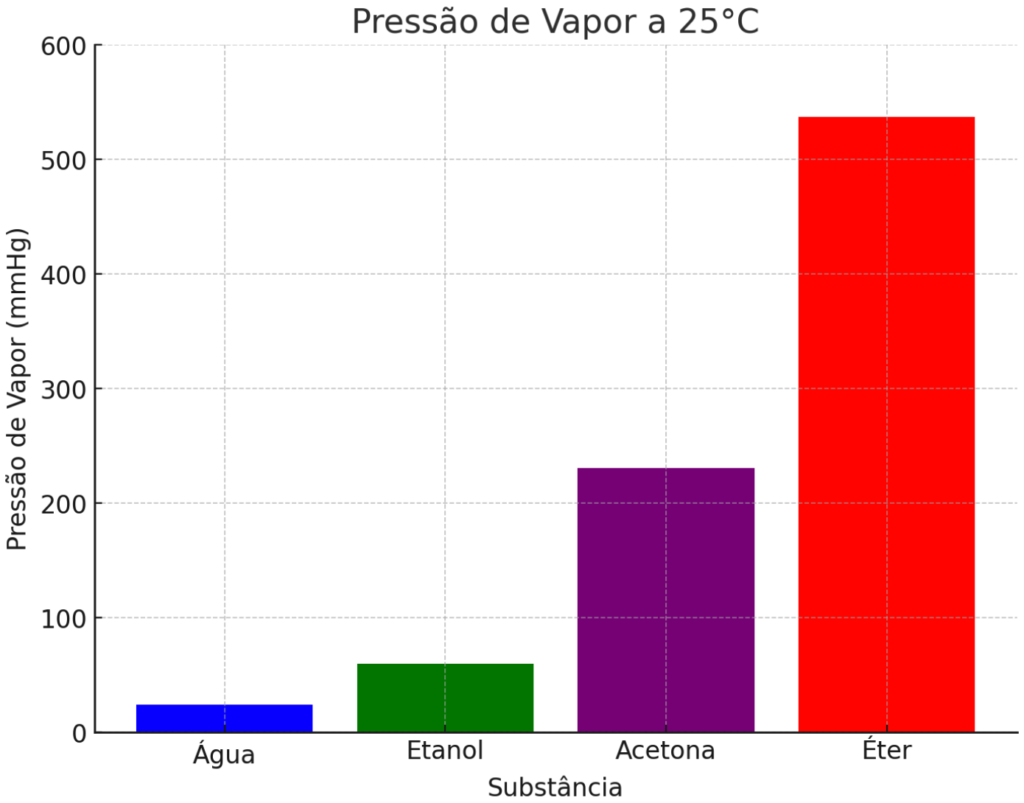
A pressão de vapor está diretamente relacionada à volatilidade de um líquido. Um líquido com maior pressão de vapor é um líquido mais volátil, pois vaporiza mais facilmente e, logo, produz mais vapor, que, por sua vez, exerce mais pressão sobre a superfície do líquido. As medidas experimentais abaixo mostram isso. As fortes ligações de hidrogênio que existem na água líquida a tornam menos volátil e, consequentemente, com menor pressão de vapor. O etanol ainda realiza ligações de hidrogênio, mas a cadeia carbônica realiza interações de natureza dispersiva e a forte rede de ligações de hidrogênio existente na água não existe para o etanol. Isso eleva a sua volatilidade e, consequentemente, sua pressão de vapor. Para a acetona, as interações dipolo-dipolo e de dispersão são bem mais fracas e isso a torna um líquido mais volátil ainda, com pressão de vapor superior aos dois primeiros. Para o éter, as interações intermoleculares são tão fracas que a pressão de vapor do éter é consideravelmente maior do que a dos demais líquidos, sendo a substância mais volátil dentre eles.
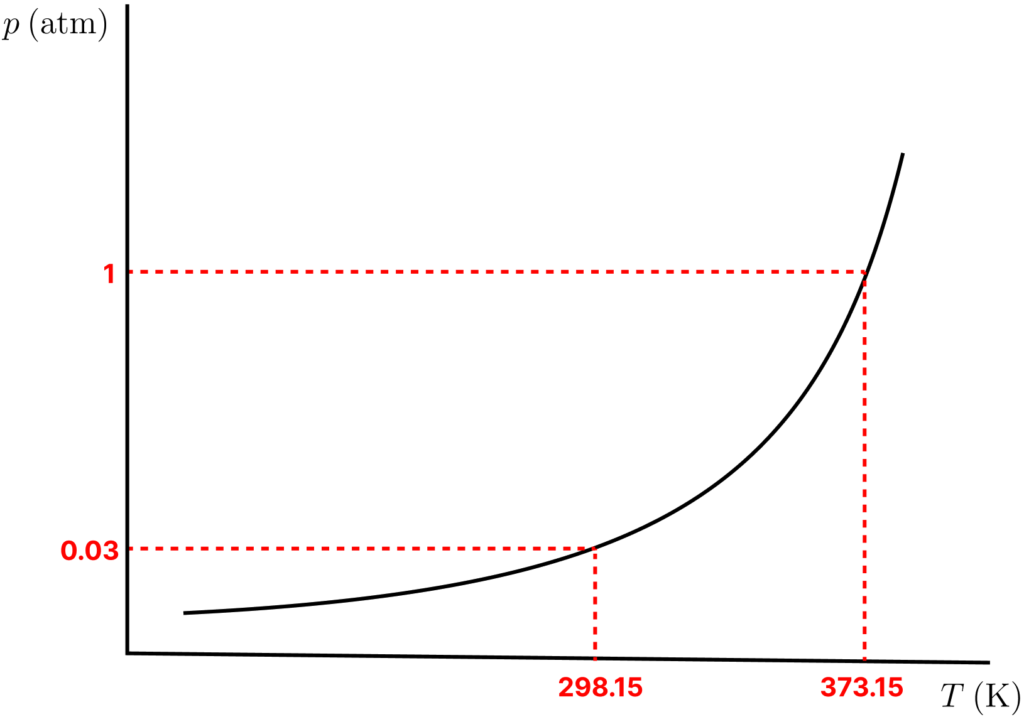
Para uma mesma substância, a pressão de vapor aumenta com a temperatura (veremos a equação que relaciona as duas grandezas em breve). A curva do aumento da pressão de vapor para a água é mostrada abaixo. Perceba que a pressão de vapor de água é ![]() (
(![]() ) na temperatura ambiente. Qualquer bolha de vapor que tente se formar nessa temperatura terá, no seu interior, uma pressão tão pequena que a pressão atmosférica de
) na temperatura ambiente. Qualquer bolha de vapor que tente se formar nessa temperatura terá, no seu interior, uma pressão tão pequena que a pressão atmosférica de ![]() a sufocará. Dessa forma, a ebulição não ocorre até que a pressão de vapor do líquido atinja o valor da pressão externa. Há duas formas disso ocorrer:
a sufocará. Dessa forma, a ebulição não ocorre até que a pressão de vapor do líquido atinja o valor da pressão externa. Há duas formas disso ocorrer:
- Aumentando a temperatura do líquido: se aquecermos o líquido, sua pressão de vapor aumenta e, na temperatura onde a sua pressão de vapor atinge o valor da pressão externa, teremos ebulição. Esse é, inclusive, o conceito de temperatura de ebulição, a temperatura na qual a pressão de vapor de um líquido atinge a pressão externa. O gráfico mostra que a pressão de vapor da água só atinge
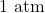 a
a 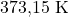 ou
ou 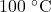 . Já vimos essa possibilidade na seta
. Já vimos essa possibilidade na seta  do último diagrama mostrado.
do último diagrama mostrado. - Diminuindo a pressão externa: se diminuirmos a pressão externa até o valor da pressão de vapor da água, uma bolha de vapor estável se formará e o líquido entra em ebulição. Veremos essa possibilidade a seguir.
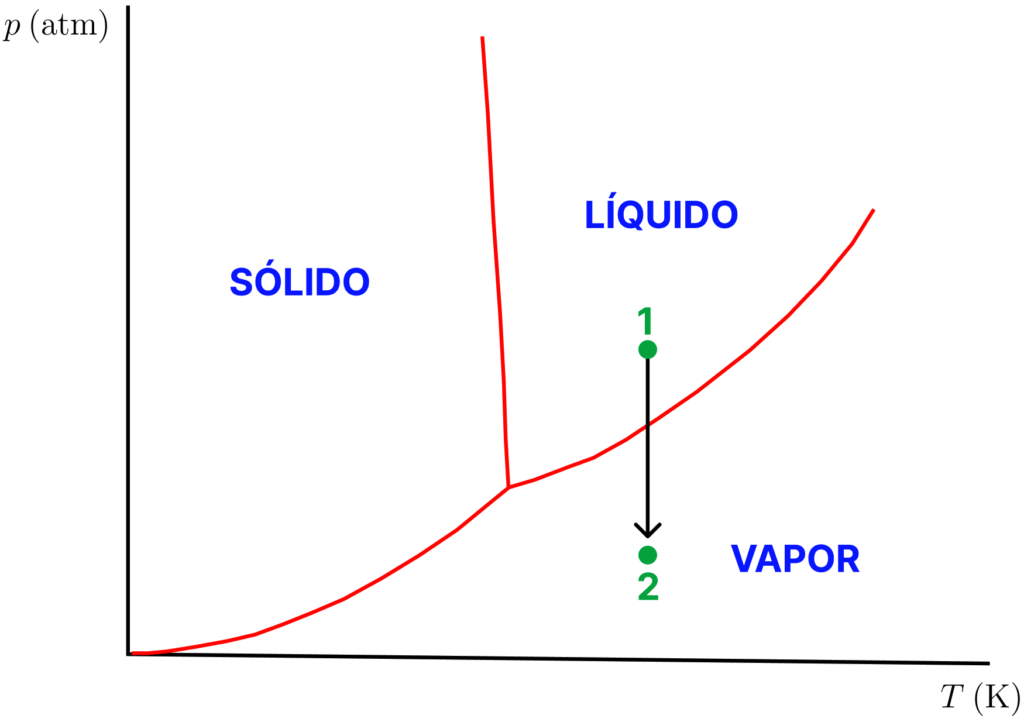
Ao diminuir a pressão externa, o estado do líquido caminha para pontos inferiores, em uma mesma linha vertical (gráfico a seguir). Ao atingir a curva LV, o líquido entra em ebulição, sem nenhum aquecimento, pois atingiu a pressão externa. Descompressão adicional fará o ponto caminhar para algo próximo ao ponto 2.
A Fusão e a Solidificação
Se tivermos um estado com uma dada pressão e temperatura dada pelo ponto 1 abaixo e o aquecermos isobaricamente (como ocorre quando removemos um cubo de gelo do congelador e o colocamos em cima da pia), a temperatura aumenta e o ponto se desloca horizontalmente para a direita, tocando a curva sólido-líquido. Quando todo o sólido fundiu, aquecimento adicional nos levará até algo próximo ao ponto 2. O resfriamento isobárico començando do ponto 2 nos levará à solidificação do líquido. Não será mostrado aqui, pela similaridade, mas, se o ponto 1 estiver abaixo do ponto triplo, o aquecimento fará a substância sublimar.

O Estado Supercrítico
Vimos que o aquecimento eleva a pressão de vapor de um líquido até que atinja a pressão externa. Porém, se o aquecimento for feito em recipiente fechado, a pressão na superfície do líquido não é a pressão externa, mas sim a pressão de vapor do líquido. Se aquecermos um líquido em recipiente fechado, o vapor formado não consegue expandir e a ebulição simplesmente não ocorre. No diagrama de fases, é como se caminhássemos sobre a linha LV para cima (figura abaixo).
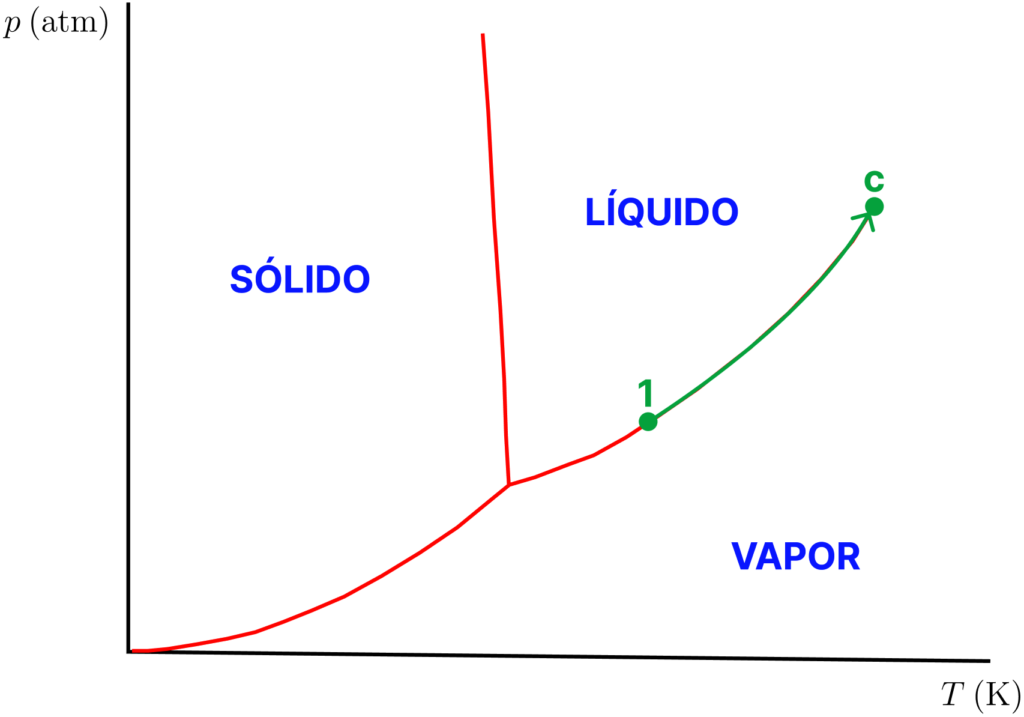
Nesse processo, o vapor torna-se cada segundo mais rico em partículas e sua densidade aumenta consideravelmente. Quando a densidade do vapor se igualar à densidade do líquido, não há mais razão para enxergarmos a superfície que os separa e estaremos diante de um fluido supercrítico. Eles são importantes devido à aplicação em estudos de extração de substâncias, fenômenos de transporte, fenômenos de superfície, química de materiais e na área médica.
A Equação de Clapeyron
Essa equação nos fornece o coeficiente angular de ![]() com
com ![]() para uma substância, ou seja,
para uma substância, ou seja, ![]() . Sua dedução envolve tomar dois pontos muito próximos e sobre uma curva de equilíbrio entre as fases
. Sua dedução envolve tomar dois pontos muito próximos e sobre uma curva de equilíbrio entre as fases ![]() e
e ![]() (figura abaixo).
(figura abaixo).
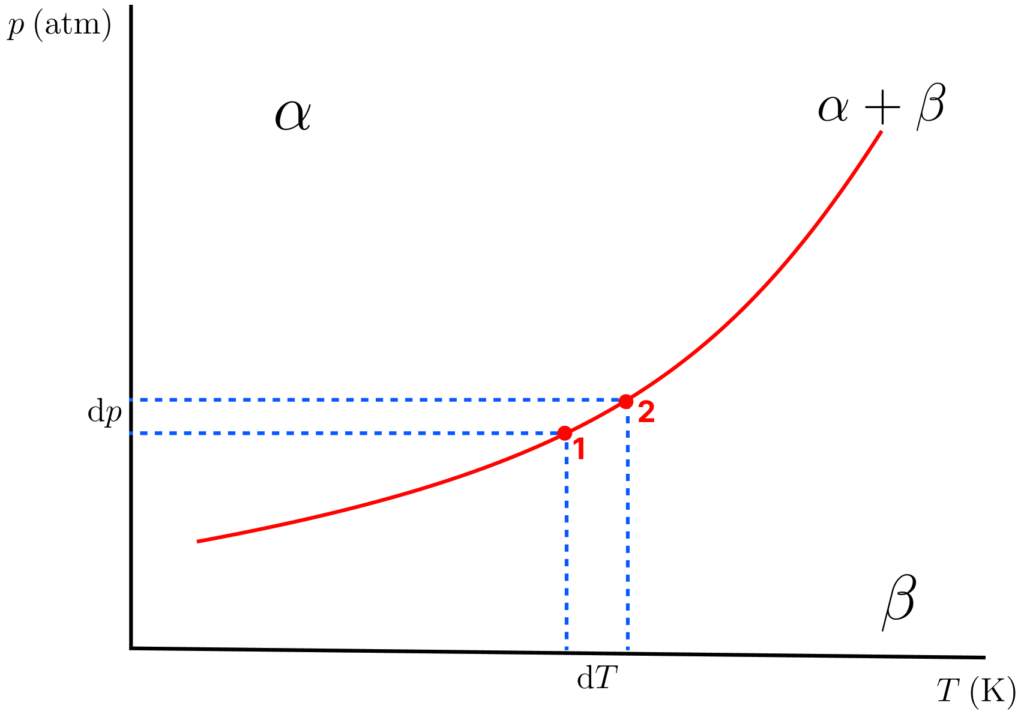
Como o equilíbrio ![]() é válido para ambos os pontos, o valor de
é válido para ambos os pontos, o valor de ![]() (
(![]() ) precisa ser o mesmo em ambos os pontos (
) precisa ser o mesmo em ambos os pontos (![]() e
e ![]() ). Assim, as mudanças de
). Assim, as mudanças de ![]() também precisam ser iguais:
também precisam ser iguais:
(26) 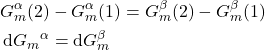
Vale lembrar que a dependência de ![]() com
com ![]() e
e ![]() é:
é:
![]()
Aplicando à equação 26:
(27) 
A equação de Clapeyron (27) é, então, uma equação exata, pois foi obtida sem quaisquer aproximações. Para a vaporização, ![]() e
e ![]() são positivos e a inclinação da curva líquido-vapor é sempre positiva. Algo semelhante acontece para as curvas sólido-vapor, mas com inclinação bem maior, porque
são positivos e a inclinação da curva líquido-vapor é sempre positiva. Algo semelhante acontece para as curvas sólido-vapor, mas com inclinação bem maior, porque ![]() .
.
A curva de equilíbrio sólido-líquido, no entanto, pode revelar surpresas. A maioria das substâncias seguem o mesmo comportamento (![]() ,
, ![]() e
e ![]() ), mas, para água, bismuto e gálio, por exemplo, a fusão provoca contração e o volume diminui (
), mas, para água, bismuto e gálio, por exemplo, a fusão provoca contração e o volume diminui (![]() ) e, como
) e, como ![]() ,
, ![]() , tornando a curva de equilíbrio sólido-líquido com inclinação negativa. Para a água esse comportamento é resultado do fato de, no gelo I, as ligações de hidrogênio serem mais longas do que no líquido, para manter o aranjo das moléculas.
, tornando a curva de equilíbrio sólido-líquido com inclinação negativa. Para a água esse comportamento é resultado do fato de, no gelo I, as ligações de hidrogênio serem mais longas do que no líquido, para manter o aranjo das moléculas.
Equilíbrios Sólido-Vapor e Líquido-Vapor
Com exceção dos pontos próximos ao estado crítico, o volume do vapor é consideravelmente maior do que o das fases condensadas. Assim, ![]() e a equação de Clapeyron se torna:
e a equação de Clapeyron se torna:
(28) 
Integrando:
(29) ![Rendered by QuickLaTeX.com \begin{align*}&\int_{p_1}^{p_2}\f{1}{p}\dd{p} \approx \f{\Delta_\text{vap}H_m}{R} \int_{T_1}^{T_2}\f{1}{T^2}\dd{T}\\&\ln{\f{p_2}{p_1}} \approx \f{\Delta_\text{vap}H_m}{R} \left[-\f{1}{T_2} + \f{1}{T_1}\right]\\&\ln{\f{p_2}{p_1}} \approx \f{\Delta_\text{vap}H_m}{R} \left[\f{1}{T_1}-\f{1}{T_2}\right]\end{align*}](https://lqtsm.com/wp-content/ql-cache/quicklatex.com-cee871aaa99f7f678bb67aefadfe6c83_l3.png)
Repare que usamos a aproximação da entalpia de transição ser constante no intervalo de temperaturas analisado, de forma que essa expressão não deve ser aplicada em maiores intervalos de temperatura. Se considerarmos ![]() ,
, ![]() e a equação se torna:
e a equação se torna:
(30) ![]()
Aplicando a exponencial em ambos os lados:
(31) ![]()
Uma forma aproximada de escrever a equação de Clapeyron para a variação da pressão de vapor com a temperatura (considerando o comportamento ideal do vapor) é:
(32) 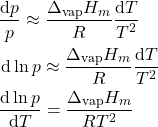
Equilíbrio Sólido-Líquido
Para o equilíbrio sólido-líquido, não podemos fazer ![]() e a equação que obtivemos não é válida aqui. Da equação de Clapeyron:
e a equação que obtivemos não é válida aqui. Da equação de Clapeyron:
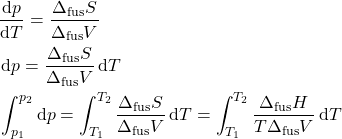
Se aproximarmos a razão \f{\Delta_\text{fus} S}{\Delta_\text{fus} V} como constante os intervalos de ![]() e
e ![]() :
:
![]()
Essa equação é válida para uma boa faixa de pressões. Um ponto importante a se considerar que é que é a equação de Clapeyron que explica o comportamento anômalo de substâncias (dentre elas a água) em ter uma curva sólido-líquido decrescente. Perceba que, da equação de Clapeyron, temos:
![]()
E todas as grandezas do lado direito dessa equação são positivas sempre, exceto ![]() . Pelo fato das moléculas de água, na solidificação, precisarem se distanciar um pouco para formar o cristal de gelo I, aumentando o volume do sólido e fazendo
. Pelo fato das moléculas de água, na solidificação, precisarem se distanciar um pouco para formar o cristal de gelo I, aumentando o volume do sólido e fazendo ![]() . Isso torna
. Isso torna ![]() e a derivada
e a derivada ![]() negativa. Perceba que isso só ocorre com o gelo I.
negativa. Perceba que isso só ocorre com o gelo I.
Transições Sólido-Sólido
É muito comum encontrarmos materiais que existem em mais de uma forma sólida. A diferença entre elas é como as partículas se organizam, formando várias estruturas cristalinas diferentes, estáveis em diferentes faixas de ![]() e
e ![]() . A capacidade que uma substância tem de existir em mais de uma fase sólida é o polimorfismo (elementos, isso é chamado de alotropia).
. A capacidade que uma substância tem de existir em mais de uma fase sólida é o polimorfismo (elementos, isso é chamado de alotropia).
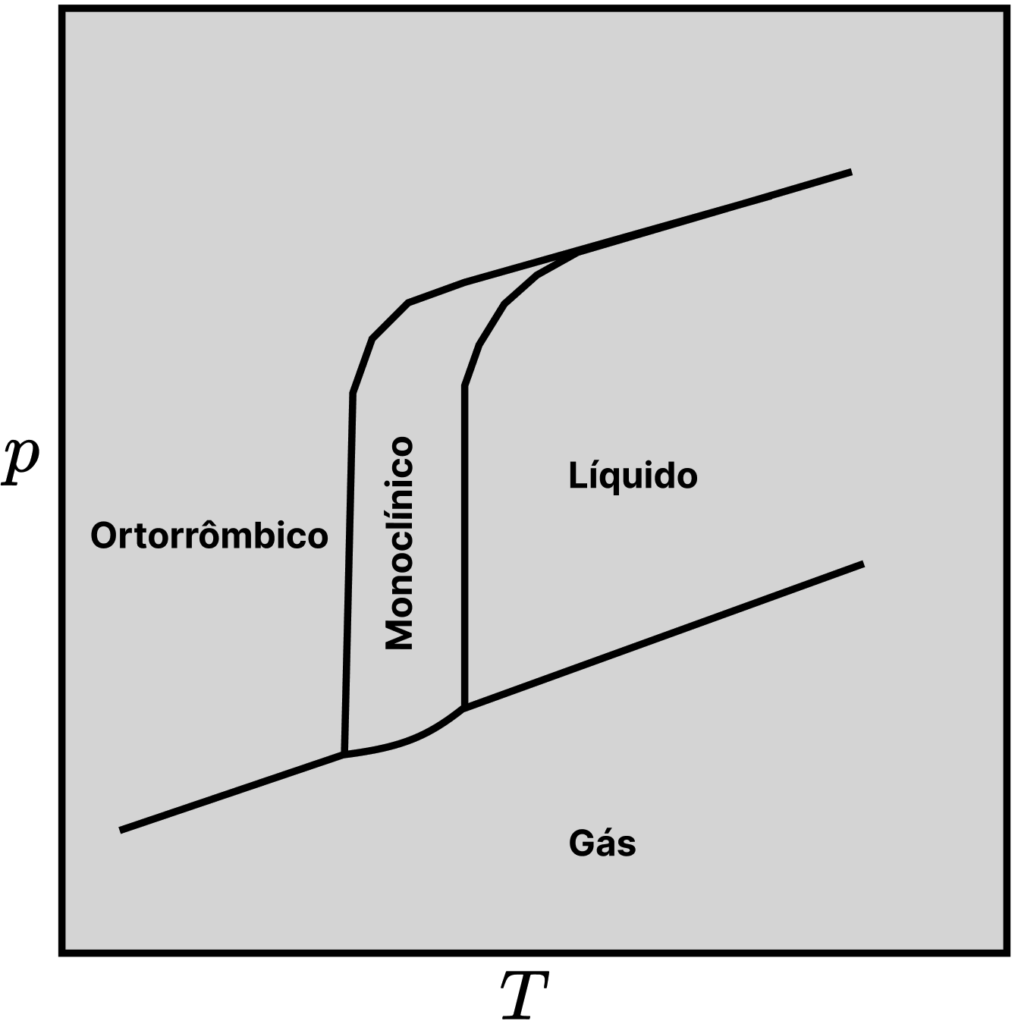
Um desses materiais é o enxofre, cuja forma ortorrômbica pode ser aquecida lentamente para gerar a forma monoclínica, em ![]() . Essa nova fase sólida entra em fusão em
. Essa nova fase sólida entra em fusão em ![]() . Esse comportamento gera três pontos triplos no diagrama, como pode ser visto na figura abaixo.
. Esse comportamento gera três pontos triplos no diagrama, como pode ser visto na figura abaixo.
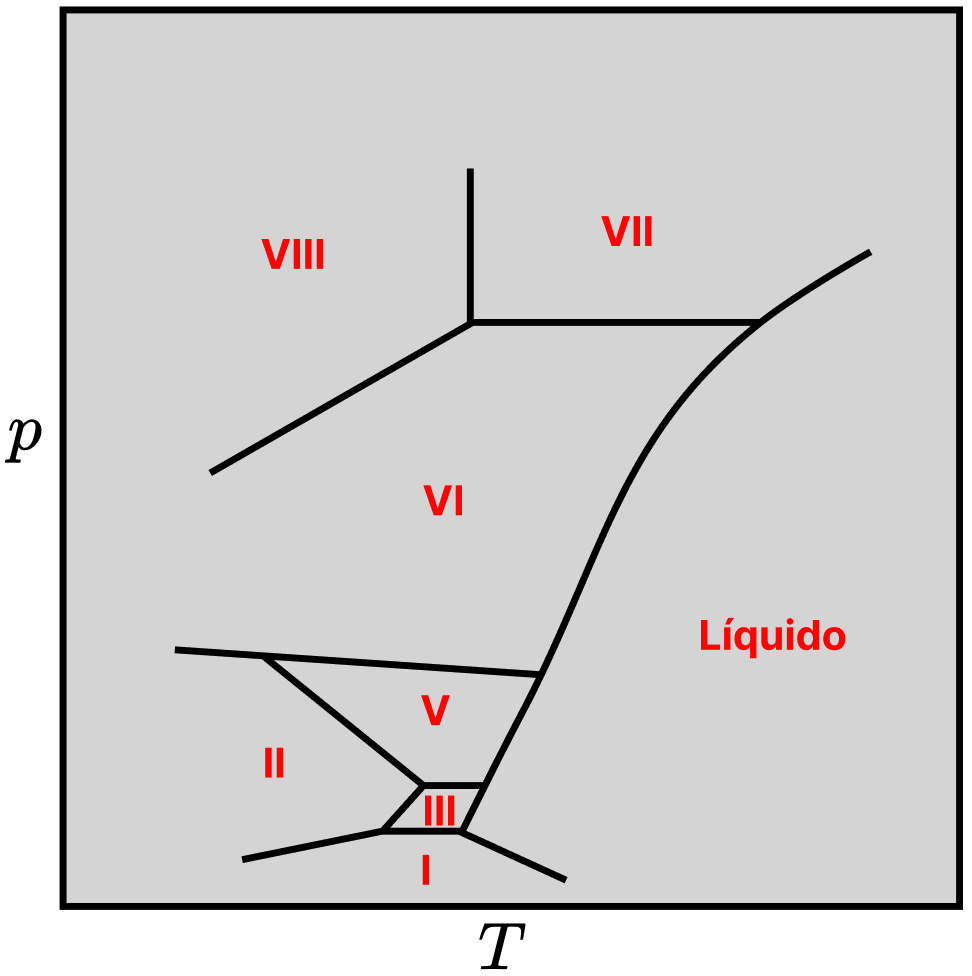
A água também apresenta várias fases sólidas. A que conhecemos e é a mais estável em baixas pressões é chamada de gelo Ih (h é uma designação do tipo de estrutura cristalina). Experimentos em altíssimas pressões revelaram que o arranjo das moléculas de água muda consideravelmente, gerando poliformos com propriedades variadas, nomeados de gelo-X, onde X é o respectivo número do polimorfo. Alguns deles não têm estrutura cristalina bem definida (são amorfos) e outros ainda estão sendo caracterizados. Abaixo está o diagrama de fases da região sólida da água.
Alguns estudos de formação e caracterização de novos polimorfos são feitos nas chamadas bigornas de diamante, que funciona colocando uma amostra entre duas faces de diamante, usando como técnica auxiliar a difração de raios X.
Exercícios
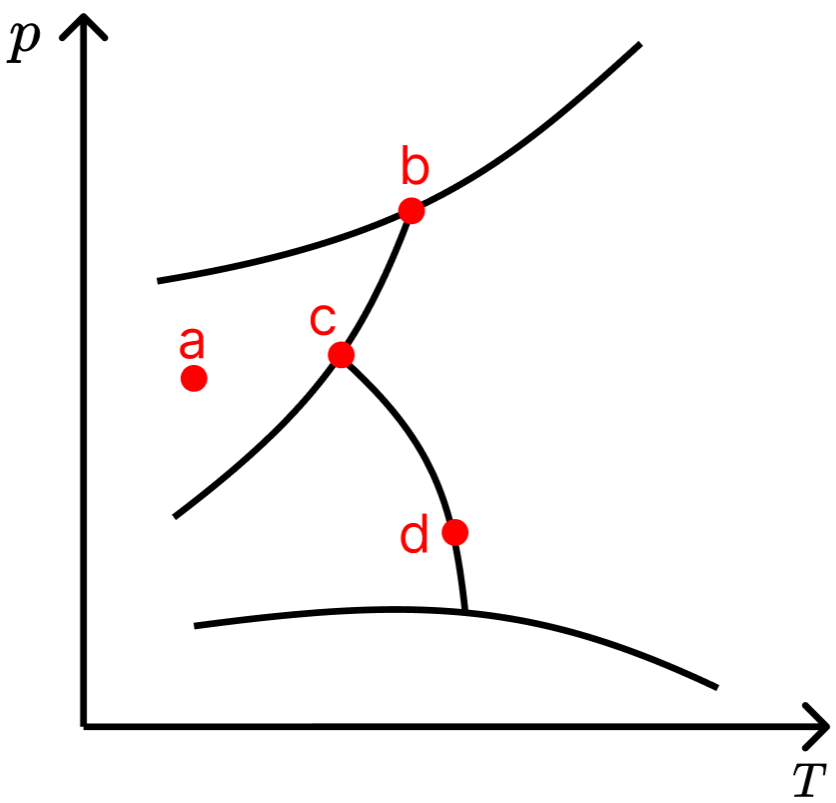
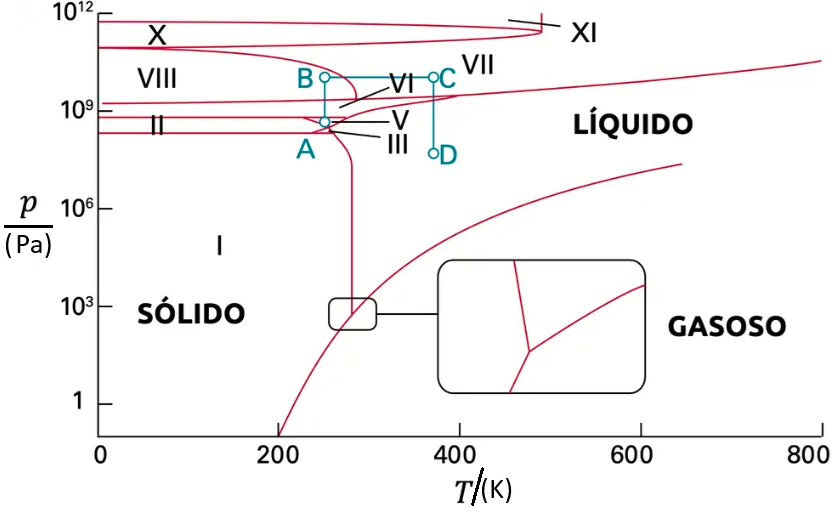
1) Quantas fases estão presentes nos pontos a, b, c e d no diagrama abaixo?
Gabarito
Ponto a: 1 fase; ponto d: 2 fases; pontos b e c: 3 fases.
Resolução
2) A diferença de potencial químico de uma substância genérica entre duas regiões de um sistema é de ![]() . Em quanto varia a energia de Gibbs quando
. Em quanto varia a energia de Gibbs quando ![]() dessa substância é transferida de uma região para outra?
dessa substância é transferida de uma região para outra?
Gabarito
![]()
Resolução
3) Qual é o número máximo de fases que podem estar em equilíbrio em um sistema de quatro componentes?
Gabarito
![]()
Resolução
4) Qual fase ou fases você esperaria estar presente para uma amostra de ![]() em:
em:
(a) ![]() e
e ![]() ;
;
(b) ![]() e
e ![]() ;
;
(c) ![]() e
e ![]() (destacado no retângulo em zoom)?
(destacado no retângulo em zoom)?
Gabarito
(a) Uma fase (gelo I).
(b) Uma fase (água líquida).
(c) Três fases (gelo I, água líquida e vapor d’água).
Resolução
5) Qual é a razão física para o aumento do potencial químico de uma substância pura à medida que a pressão aumenta?
Gabarito
![]() , Como a derivada do potencial químico em relação à pressão é o volume molar (que é sempre positivo),
, Como a derivada do potencial químico em relação à pressão é o volume molar (que é sempre positivo), ![]() sempre cresce com
sempre cresce com ![]() .
.
Resolução
6) A entropia molar padrão da água líquida a ![]() é
é ![]() , e a do gelo na mesma temperatura é
, e a do gelo na mesma temperatura é ![]() . Calcule a mudança no potencial químico da água líquida e do gelo quando a temperatura é decrescida em
. Calcule a mudança no potencial químico da água líquida e do gelo quando a temperatura é decrescida em ![]() a partir do ponto de fusão normal. Dando suas razões, explique qual fase é termodinamicamente a mais estável na nova temperatura.
a partir do ponto de fusão normal. Dando suas razões, explique qual fase é termodinamicamente a mais estável na nova temperatura.
Gabarito
![]() , Como o potencial químico do líquido aumenta mais do que o do sólido, a fase sólida é mais estável na nova temperatura.
, Como o potencial químico do líquido aumenta mais do que o do sólido, a fase sólida é mais estável na nova temperatura.
Resolução
7) Em quanto o potencial químico do benzeno muda quando a pressão exercida sobre uma amostra é aumentada de ![]() para
para ![]() ? Tome a densidade de massa do benzeno para
? Tome a densidade de massa do benzeno para ![]() .
.
Gabarito
![]()
Resolução
8) A pressão de vapor de uma substância a ![]() é de
é de ![]() e sua entalpia de vaporização é de
e sua entalpia de vaporização é de ![]() . Estime a temperatura na qual sua pressão de vapor é de
. Estime a temperatura na qual sua pressão de vapor é de ![]() .
.
Gabarito
![]()
Resolução
9) Descobriu-se que a pressão de vapor de um líquido na faixa de temperatura ![]() se encaixa na expressão
se encaixa na expressão ![]() . Qual é a entalpia da vaporização do líquido?
. Qual é a entalpia da vaporização do líquido?
Gabarito
![]()
Resolução
10) Quando um determinado líquido (com ![]() ) congela a
) congela a ![]() e a
e a ![]() , sua densidade de massa muda de
, sua densidade de massa muda de ![]() para
para ![]() . Sua entalpia de fusão é de
. Sua entalpia de fusão é de ![]() . Estime o ponto de congelamento do líquido em
. Estime o ponto de congelamento do líquido em ![]() .
.
Gabarito
![]()
