A Direção da Mudança Espontânea
A primeira lei da termodinâmica restringe os processos àqueles que ocorrem com conservação de energia. Assim, se a energia interna do sistema diminuir, ou calor foi trocado ou trabalho foi realizado (ou os dois). Nos concentraremos agora em outra discussão: a direção espontânea de uma transformação.
Qualquer sistema que ainda não atingiu o equilíbrio precisa evoluir espontaneamente para tal. Cuidado com o significado da palavra espontânea. Uma transformação ser espontânea não significa que sua ocorrência é imediata e rápida. Essas duas qualidades são preocupações da cinética e não da termodinâmica.
A “direção espontânea” indica que a transformação tem maior probabilidade de ocorrer nesta direção do que na oposta. A segunda lei da termodinâmica (que será apresentada formalmente em breve) nos ajuda a prever a direção espontânea de uma transformação.
Exemplos Ilustrativos
Considere a bola que cai em um campo gravitacional e salta para cima depois de colidir com o chão.
No início, a bola concentra uma grande quantidade de energia potencial. A queda transforma energia potencial em cinética e parte dessa energia é deixada no solo no choque inelástico, ou seja, parte da energia é distribuída ao movimento das partículas do solo. Quando a queda espontânea ocorre até o fim, toda a energia que estava inicialmente armazenada na bola está, agora, dispersa por todo o sistema. Imagine o processo na direção oposta. Uma bolinha inicialmente em repouso, no solo e, repentinamente, começa a pular até atingir uma certa altura.
Nossa intuição nos diz que esse processo não é espontâneo. Para isso ocorrer, seria necessário que a energia de partículas do solo se concentrassem em um único ponto (que deve ser a localização da bola), impulsionando-a para cima. A probabilidade desse processo ocorrer é desprezível e dizemos que ela não é espontânea. Assim, o sentido da transformação espontânea parece estar associado ao grau de dispersão da energia. Imaginemos, ainda, um segundo exemplo: duas peças metálicas em temperaturas diferentes (
).
Nossa experiência diária nos leva a pensar que a peça quente será resfriada e a peça fria será aquecida, até que o conjunto inteiro tenha a mesma temperatura (equilíbrio térmico). A direção oposta é, certamente, não espontânea. Duas barras em equilíbrio térmico não evoluem espontaneamente para que uma tenha temperatura superior à outra. Mais uma vez, a direção espontânea parece ser governada pela maior dispersão da energia. A dispersão não ocorre apenas com a energia, mas, também, com a matéria. Imagine a expansão de Joule, vista em alguns tópicos atrás. A direção espontânea é a da expansão do gás contra o vácuo, dispersando as partículas pelos dois recipientes.
section{Definição Termodinâmica da Entropia}
Para quantificar o grau de dispersão e desordem da energia e da matéria, uma nova função de estado será definida. A definição que apresentaremos aqui é operacional, de modo que será focada na mudança dessa nova função de estado (chamada de entropia) para um processo (
), que é definida por:
begin{align*}
dd S = dfrac{dd q_text{rev}}{T} label{S_def}
end{align*}
- Onde:
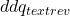é a energia transferida como calor reversivelmente.
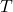é a temperatura na qual ocorre o processo reversível.
À primeira vista, a expressão sugere que só é possível calcular variações de entropia para processos reversíveis. Contudo, podemos calcular variações de entropia para processos irreversíveis também, desde que encontremos um caminho alternativo e reversível que conecte os mesmos estados inicial e final. Como 
é uma função de estado, o resultado de 
encontrado para o caminho alternativo reversível será o mesmo para o processo irreversível desejado. É preciso, apenas, tomar cuidado de não usar 
do processo irreversível, pois a razão 
só é igual à 
se o processo é reversível. Se usarmos a razão 
para processos irreversíveis, encontraremos uma entropia superestimada, porque leva em conta variações de entropia do sistema e variações de entropia imprevisíveis, devido à irreversibilidade do processo. Com isso, definimos a desigualdade de Clausius:
begin{align*}
& dd S ge frac{dd q}{T} qquad text{Desigualdade de Clausius}
end{align*}
Nessa desigualdade, o sinal de igualdade vale apenas para processos reversíveis e o sinal de maior vale para processos irreversíveis.
Os processos que realizamos em laboratório envolvem quantidades macroscópicas e não infinitesimalmente pequenas como 
. Assim, para calcular a variação de entropia de um “macroprocesso” é preciso dividi-lo em infinitos microprocessos, de forma que, quando cada microprocesso ocorrer, damos tempo para que o equilíbrio seja atingido. Se quisermos, ao longo dos vários microprocessos, reverter o processo, basta variar infinitesimalmente alguma propriedade. Como resultado, o macroprocesso hipotético que acabamos de criar é reversível ou quase-estáticos, que não existe em um laboratório real, mas é útil para calcular propriedades termodinâmicas. Para um processo reversível, a variação de entropia é:
begin{align*}
Delta S = int_{i}^{f}dfrac{dd q_{text{rev}}}{T}
end{align*}
A unidade de entropia, no sistema internacional, é o 
. A unidade de entropia molar (
), no sistema internacional, é o 
.