Entropia, Espontaneidade e Equilíbrio
Vamos supor que um sistema ainda não tenha atingido o equilíbrio, isto é, ainda existem reações químicas, mudanças de fase ou qualquer processo que precisa evoluir espontaneamente para um equilíbrio. O que governa esse processo espontâneo é a maximização de ![]() (
(![]() ). Quando essa soma atinge seu valor máximo, o sistema entra em equilíbrio, de modo que, a partir deste momento, nenhum processo parece continuar ocorrendo (apesar de sabermos que o equilíbrio é microscopicamente dinâmico).
). Quando essa soma atinge seu valor máximo, o sistema entra em equilíbrio, de modo que, a partir deste momento, nenhum processo parece continuar ocorrendo (apesar de sabermos que o equilíbrio é microscopicamente dinâmico).
Quando esse equilíbrio é atingido, qualquer processo que tente ocorrer irá diminuir ![]() , o que é proibido pela segunda lei. A única forma de alterar o sistema a partir desse ponto é de forma infinitesimal, ou seja, variando tão pouco uma dada propriedade que, a qualquer momento, você pode mudar a direção do processo. Esse processo reversível é um processo apenas idealizado, mas, se ocorrer, irá levar o sistema até um ponto muito próximo ao de entropia máxima. Para este processo:
, o que é proibido pela segunda lei. A única forma de alterar o sistema a partir desse ponto é de forma infinitesimal, ou seja, variando tão pouco uma dada propriedade que, a qualquer momento, você pode mudar a direção do processo. Esse processo reversível é um processo apenas idealizado, mas, se ocorrer, irá levar o sistema até um ponto muito próximo ao de entropia máxima. Para este processo:
(1) ![]()
Para processos irreversíveis, infelizmente não podemos usar a razão ![]() para calcular
para calcular ![]() . Isso ocorre porque o caráter irreversível traz contribuições adicionais de entropia que são muito difíceis de contabilizar. Essa parcela adicional à
. Isso ocorre porque o caráter irreversível traz contribuições adicionais de entropia que são muito difíceis de contabilizar. Essa parcela adicional à ![]() (devido à irreversibilidade) é a razão da desigualdade de Clausius (equação 2).
(devido à irreversibilidade) é a razão da desigualdade de Clausius (equação 2).
(2) ![]()
Onde a igualdade é válida apenas para processos reversíveis e o sinal de maior é para processos irreversíveis. Da primeira lei:
![]()
Da desigualdade de Clausius, ![]() e a equação acima se torna:
e a equação acima se torna:
![]()
Onde o sinal de igualdade só se aplica ao equilíbrio (![]() ) e o de desigualdade, ao processo irreversível (
) e o de desigualdade, ao processo irreversível (![]() ).
).
A Energia Livre de Helmholtz
Vamos discutir, primeiramente, espontaneidade e equilíbrio para sistemas mantidos em ![]() e
e ![]() constantes. A equação que obtivemos (
constantes. A equação que obtivemos (![]() ) pode ser reescrita como:
) pode ser reescrita como:
![]()
Podemos fazer surgir a diferencial ![]() somando e subtraindo
somando e subtraindo ![]() do lado direito:
do lado direito:
![]()
Pela regra da cadeia: ![]() . Assim, a equação acima pode ser reescrita como:
. Assim, a equação acima pode ser reescrita como:
![]()
Como estamos lidando com sistemas mantidos a ![]() e
e ![]() fixos, temos que
fixos, temos que ![]() e
e ![]() e:
e:
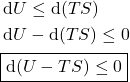
Essa equação significa que um processo espontâneo que ocorre em um sistema mantido a ![]() e
e ![]() fixos sempre minimiza a coleção a combinação “
fixos sempre minimiza a coleção a combinação “![]() “. Para sistemas em equilíbrio,
“. Para sistemas em equilíbrio, ![]() é um mínimo e qualquer processo adicional será não espontâneo, diminuindo a entropia total. Essa função
é um mínimo e qualquer processo adicional será não espontâneo, diminuindo a entropia total. Essa função ![]() é conhecida como a energia livre de Helmhtolz, definida como na equação 3.
é conhecida como a energia livre de Helmhtolz, definida como na equação 3.
(3) ![]()
A Energia Livre de Gibbs (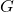 )
)
Vamos considerar agora um sistema mantido a ![]() e
e ![]() constantes (
constantes (![]() e
e ![]() nulos). Vimos que:
nulos). Vimos que:
![]()
Para introduzir ![]() e
e ![]() , completamos a expressão da regra da cadeia de
, completamos a expressão da regra da cadeia de ![]() e
e ![]() , adicionando e subtraindo
, adicionando e subtraindo ![]() e
e ![]() :
:
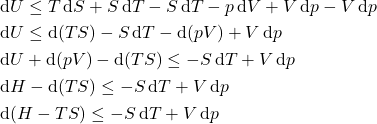
Aplicando a condição de ![]() e
e ![]() serem mantidos constantes:
serem mantidos constantes:
![]()
Mais uma vez o sinal de igualdade é para processos reversíveis e o de desigualdade vale para processos irreversíveis. Dessa forma, parece ser a coleção de funções de estado ![]() que governa espontaneidade e equilíbrio em sistemas mantidos a
que governa espontaneidade e equilíbrio em sistemas mantidos a ![]() e
e ![]() constantes. Essa coleção é uma nova função de estado: a energia livre de Gibbs
constantes. Essa coleção é uma nova função de estado: a energia livre de Gibbs ![]() (definido na equação 4), que precisa atingir um mínimo em processos espontâneos.
(definido na equação 4), que precisa atingir um mínimo em processos espontâneos.
(4) ![]()
Aqui vale uma pequena pausa para colocar as ideias no lugar. O descritor de espontaneidade e equilíbrio é sempre a entropia total (sua maximização). Como ela contabiliza quantidades relacionadas às vizinhanças, definimos duas novas funções de estado (![]() e
e ![]() ) do sistema, que, em condições especiais, fazem a mesma coisa que
) do sistema, que, em condições especiais, fazem a mesma coisa que ![]() , ou seja, descrevem espontaneidade e equilíbrio, mas sem precisarmos olhar para as vizinhanças e sim para
, ou seja, descrevem espontaneidade e equilíbrio, mas sem precisarmos olhar para as vizinhanças e sim para ![]() ou
ou ![]() do sistema.
do sistema.
Mas cuidado. Você só pode usar ![]() para descrever espontaneidade e equilíbrio em sistemas mantidos a
para descrever espontaneidade e equilíbrio em sistemas mantidos a ![]() e
e ![]() fixos. Similarmente, você só pode usar
fixos. Similarmente, você só pode usar ![]() para tal se o sistema estiver a
para tal se o sistema estiver a ![]() e
e ![]() fixos. Se nenhuma dessas condições for verdadeira, volte sempre ao “lar” e use
fixos. Se nenhuma dessas condições for verdadeira, volte sempre ao “lar” e use ![]() , válida para qualquer situação (lidar com as vizinhanças agora é a dificuldade). Mas não desanime, as condições
, válida para qualquer situação (lidar com as vizinhanças agora é a dificuldade). Mas não desanime, as condições ![]() constantes e
constantes e ![]() constantes são bem comuns em química. A segunda é ainda mais comum, pois reações feitas em recipientes abertos (submetidos à pressão atmosférica) e com pouca variação de temperatura são descritas em termos de
constantes são bem comuns em química. A segunda é ainda mais comum, pois reações feitas em recipientes abertos (submetidos à pressão atmosférica) e com pouca variação de temperatura são descritas em termos de ![]() .
.
Os gráficos abaixo mostram a evolução de ![]() e
e ![]() ao longo de um processo espontâneo e irreversível (minimização da energia livre) até atingir o equilíbrio (mínimo da energia livre), onde passa a ser reversível pela variação infinitesimal de alguma propriedade.
ao longo de um processo espontâneo e irreversível (minimização da energia livre) até atingir o equilíbrio (mínimo da energia livre), onde passa a ser reversível pela variação infinitesimal de alguma propriedade.
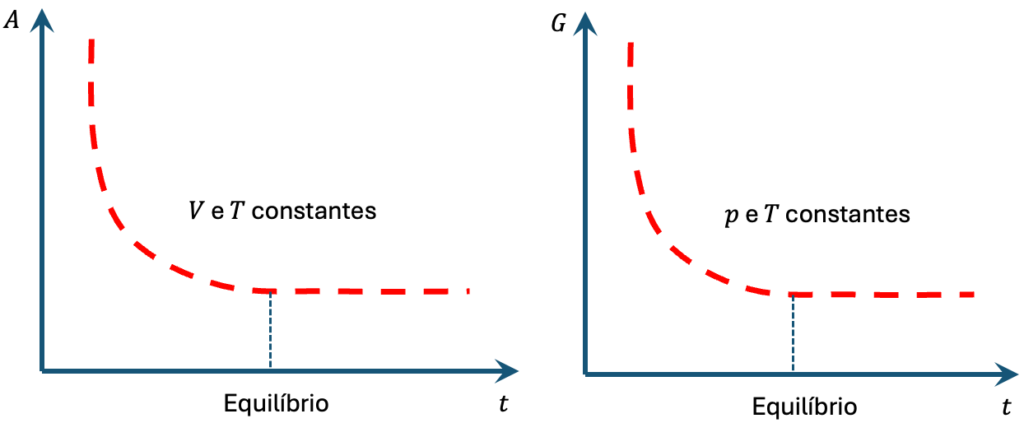
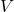 e
e 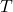 fixos) e de Gibbs (a
fixos) e de Gibbs (a 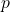 e
e 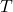 fixos) durante um processo espontâneo.
fixos) durante um processo espontâneo.É importante enfatizar que qualquer sistema possui ![]() e
e ![]() , e não apenas aqueles mantidos a
, e não apenas aqueles mantidos a ![]() e
e ![]() fixos. Porém, eles só são descritores de espontaneidade e equilíbrio nessas condições citadas. Outro ponto que merece destaque é que a primeira lei estabelece uma conservação de energia, ou seja,
fixos. Porém, eles só são descritores de espontaneidade e equilíbrio nessas condições citadas. Outro ponto que merece destaque é que a primeira lei estabelece uma conservação de energia, ou seja, ![]() precisa ser sempre constante (mesmo que haja troca de calor ou realização de trabalho). Apesar de
precisa ser sempre constante (mesmo que haja troca de calor ou realização de trabalho). Apesar de ![]() e
e ![]() terem unidades de energia (
terem unidades de energia (![]() , no S.I.), elas não precisam ser conservadas, ou seja,
, no S.I.), elas não precisam ser conservadas, ou seja, ![]() e
e ![]() não precisam ser constantes.
não precisam ser constantes.
A temperatura figura nas equações de ![]() e
e ![]() e, como as condições citadas (
e, como as condições citadas (![]() e
e ![]() fixos) contém
fixos) contém ![]() , vale a pena citar a variação de
, vale a pena citar a variação de ![]() e
e ![]() em temperatura constante (
em temperatura constante (![]() ). Para
). Para ![]() :
:
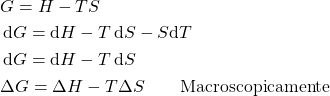
Para ![]() :
:
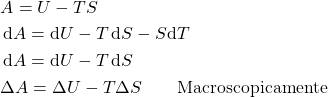
Como citado anteriormente, usar ![]() ou
ou ![]() (
(![]() fixos) fornece discussões equivalentes, então deve existir uma relação matemática entre
fixos) fornece discussões equivalentes, então deve existir uma relação matemática entre ![]() e
e ![]() .
.
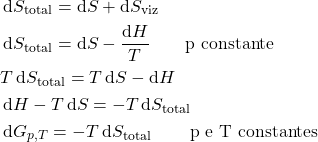
Ou, macroscopicamente:
![]()
Semelhantemente:
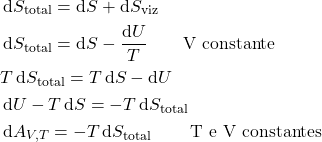
Macroscopicamente:
![]()
Nomenclatura
Vimos que:
![]()
O lado esquerdo é conhecido (![]() , para
, para ![]() fixo).
fixo).
![]()
Para processos reversíveis (onde o trabalho é máximo), vale o sinal de igualdade, então:
![]()
O significado deste expressão é que a variação da energia de Helmholtz é o trabalho máximo e esta é a razão de ![]() ser chamado de função trabalho.
ser chamado de função trabalho.
Para ![]() :
:
![]()
Porém, ![]() e:
e:
![]()
Se o processo ocorrer a ![]() e
e ![]() constante:
constante:
![]()
Esse trabalho ![]() pode ser separado nas contribuições de expansão (
pode ser separado nas contribuições de expansão (![]() ) e de não expansão (
) e de não expansão (![]() ). Assim:
). Assim:
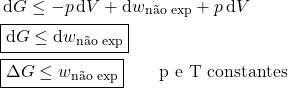
A equação acima significa que a variação da energia livre de Gibbs é o trabalho máximo de não expansão sob ![]() e
e ![]() constantes. Esse tipo de trabalho é últil em pilhas, por exemplo, que funcionam em
constantes. Esse tipo de trabalho é últil em pilhas, por exemplo, que funcionam em ![]() e
e ![]() constantes, realizando trabalho elétrico (de não expansão). Outro contexto, é o trabalho realizado pelo corpo humano em suas atividades diárias (andar, correr, levantar peso, …). Neste caso, é útil calcular o
constantes, realizando trabalho elétrico (de não expansão). Outro contexto, é o trabalho realizado pelo corpo humano em suas atividades diárias (andar, correr, levantar peso, …). Neste caso, é útil calcular o ![]() da reação global do ciclo de Krebs, associada ao consumo de glicose no corpo humano.
da reação global do ciclo de Krebs, associada ao consumo de glicose no corpo humano.
Energia de Gibbs Molar Padrão de Reação (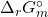 )
)
Assim como fizemos para a entalpia de uma reação, a energia de Gibbs padrão de reação é a variação da energia de Gibbs da transformação de reagentes a ![]() em produtos a
em produtos a ![]() .
.
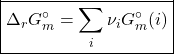
![]() é a energia de Gibbs de
é a energia de Gibbs de ![]() de uma substância, a
de uma substância, a ![]() . Essa grandeza é difícil de determinar experimentalmente, pois seria necessário medir a energia interna do sistema (
. Essa grandeza é difícil de determinar experimentalmente, pois seria necessário medir a energia interna do sistema (![]() ), que é uma soma de contribuições de energia cinética e potencial de todas as
), que é uma soma de contribuições de energia cinética e potencial de todas as ![]() do sistema.
do sistema.
![]()
Assim como fizemos para a entalpia, usaremos aqui a energia de Gibbs padrão de formação (![]() ), associada à variação da energia de Gibbs da transformação de substâncias simples, na sua forma de referência e a
), associada à variação da energia de Gibbs da transformação de substâncias simples, na sua forma de referência e a ![]() , em
, em ![]() do composto puro e a
do composto puro e a ![]() . A tabela abaixo mostra as energia de Gibbs de formação de algumas substâncias.
. A tabela abaixo mostra as energia de Gibbs de formação de algumas substâncias.
| Composto | |
Assim, podemos determinar o ![]() de qualquer reação usando o fato de que
de qualquer reação usando o fato de que ![]() é uma função de estado. No lugar de usar o processo original, mudaremos o caminho para:
é uma função de estado. No lugar de usar o processo original, mudaremos o caminho para:
![]()
A soma desses dois processos resultará em ![]() , que é a conhecida expressão “Produtos – Reagentes”, escrita de maneira mais formal como:
, que é a conhecida expressão “Produtos – Reagentes”, escrita de maneira mais formal como:
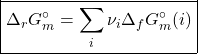
Para finalizar, assim como foi feito para a entalpia, a energia de Gibbs padrão de formação de íons é determinada escolhendo um íon de referência (o ![]() ) na fase aquosa. Assim:
) na fase aquosa. Assim:
![]()
Exercícios
Questão 1)
Dados os dados abaixo (todos em ![]() ), calcule a energia de Gibbs padrão nessa mesma temperatura para a reação equacionada por:
), calcule a energia de Gibbs padrão nessa mesma temperatura para a reação equacionada por:
![]()
Resposta
![]()
Resolução
Questão 2)
Calcule a energia padrão de Gibbs para a reação equacionada por ![]() a
a ![]() .
.
Resposta
![]()
Resolução
Questão 3)
A entalpia padrão de combustão de etanoato de etila líquido (acetato de etila, ![]() ) é de
) é de ![]() a
a ![]() e sua entropia molar padrão é de
e sua entropia molar padrão é de ![]() . Calcule a energia padrão de Gibbs de formação do composto em
. Calcule a energia padrão de Gibbs de formação do composto em ![]() usando os dados fornecidos nas tabelas abaixo (todos em
usando os dados fornecidos nas tabelas abaixo (todos em ![]() ).
).
Resposta
![]()
Resolução
Questão 4)
O tipo de biomolécula que, ao ser digerida, produz mais energia são os carboidratos. A Sociedade Brasileira de Nutrição recomenda a ingestão diária de ![]() de glicose por quilograma de peso corporal. Suponha que uma pessoa de
de glicose por quilograma de peso corporal. Suponha que uma pessoa de ![]() ingira o triplo da quantidade de glicose recomendada e que, para manter as atividades físicas diárias, essa pessoa precise de
ingira o triplo da quantidade de glicose recomendada e que, para manter as atividades físicas diárias, essa pessoa precise de ![]() de trabalho muscular. Quanto de energia sobrará?
de trabalho muscular. Quanto de energia sobrará?
| Substância | |
| Gás carbônico | |
| Água líquida | |
| Glicose |
Resposta
![]() (irreal).
(irreal).
Resolução
Questão 5)
Considere que ![]() de gás nitrogênio (comportamento ideal) possa sofrer expansão de um volume inicial de
de gás nitrogênio (comportamento ideal) possa sofrer expansão de um volume inicial de ![]() para um volume final de
para um volume final de ![]() das seguintes formas:
das seguintes formas:
(a) livre.
(b) contra uma pressão externa constante de ![]() .
.
(c) isotermicamente (![]() ), contra uma pressão externa variável, que se ajusta à pressão interna para manter a reversibilidade.
), contra uma pressão externa variável, que se ajusta à pressão interna para manter a reversibilidade.
Calcule o trabalho de expansão em cada caso e a variação da energia livre de Helmholtz da expansão descrita na letra (c).
Resposta
(a) ![]()
(b) ![]()
(c) ![]()
Resolução
Questão 6)
Em células biológicas, a energia liberada pela oxidação dos alimentos é armazenada em trifosfato de adenosina (ATP ou ![]() ). A essência da ação do ATP é sua capacidade de perder seu grupo fosfato terminal por hidrólise e formar difosfato de adenosina (ADP ou
). A essência da ação do ATP é sua capacidade de perder seu grupo fosfato terminal por hidrólise e formar difosfato de adenosina (ADP ou ![]() ):
):
![]()
Em ![]() e
e ![]() , a entalpia e a energia livre de Gibbs de hidrólise são
, a entalpia e a energia livre de Gibbs de hidrólise são ![]() e
e ![]() , respectivamente. Nessas condições, a hidrólise de
, respectivamente. Nessas condições, a hidrólise de ![]() de
de ![]() resulta na extração de até
resulta na extração de até ![]() de energia que pode ser usada para trabalhos não-expansivos, como a síntese de proteínas a partir de aminoácidos, contração muscular e ativação de circuitos neuronais em nosso cérebro.
de energia que pode ser usada para trabalhos não-expansivos, como a síntese de proteínas a partir de aminoácidos, contração muscular e ativação de circuitos neuronais em nosso cérebro.
(a) Calcule e explique o sinal da entropia de hidrólise de ATP em ![]() e
e ![]() .
.
(b) Suponha que o raio de uma célula biológica típica seja ![]() e que dentro dela
e que dentro dela ![]() moléculas de ATP são hidrolisadas a cada segundo. Qual é a densidade de potência da célula em watts por metro cúbico?
moléculas de ATP são hidrolisadas a cada segundo. Qual é a densidade de potência da célula em watts por metro cúbico?
(c) Uma bateria de computador fornece cerca de ![]() e tem um volume de
e tem um volume de ![]() . Quantas células biológicas são necessárias para gerar uma densidade de energia igual ao da bateria de computador?
. Quantas células biológicas são necessárias para gerar uma densidade de energia igual ao da bateria de computador?
(d) A formação de glutamina a partir de glutamato e íons amônio exige ![]() de entrada de energia como trabalho. É conduzida pela hidrólise de ATP a ADP mediada pela enzima glutamina sintetase. Quantos mols de ATP devem ser hidrolisados para formar
de entrada de energia como trabalho. É conduzida pela hidrólise de ATP a ADP mediada pela enzima glutamina sintetase. Quantos mols de ATP devem ser hidrolisados para formar ![]() de glutamina?
de glutamina?
Resposta
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
Resolução
Correção no vídeo. A unidade de entropia é ![]()
